题目内容
设S是不等式x2-x-6≤0的解集,整数m,n∈S。
(1)记“使得m+n=0成立的有序数组(m,n)”为事件A,试列举A包含的基本事件;
(2)设ξ=m2,求ξ的分布列及其数学期望E(ξ)。
(1)记“使得m+n=0成立的有序数组(m,n)”为事件A,试列举A包含的基本事件;
(2)设ξ=m2,求ξ的分布列及其数学期望E(ξ)。
解:(1)由x2-x-6≤0得-2≤x≤3,
即S={x|-2≤x≤3}
由于m,n∈Z,m,n∈S且m+n=0
所以A包含的基本事件为:
(-2,2),(2,-2),(-1,1),(1,-1),(0,0)。
(2)由于m的所有不同取值为-2,-1,0,1,2,3,
所以ξ=m2的所有不同取值为0,1,4,9,
且有P(ξ=0)= ,
,
P(ξ=1)=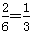 ,
,
P(ξ=4)=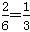 ,
,
P(ξ=9)=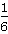
故ξ的分布列为:
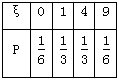
所以E(ξ)=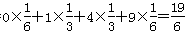 。
。
即S={x|-2≤x≤3}
由于m,n∈Z,m,n∈S且m+n=0
所以A包含的基本事件为:
(-2,2),(2,-2),(-1,1),(1,-1),(0,0)。
(2)由于m的所有不同取值为-2,-1,0,1,2,3,
所以ξ=m2的所有不同取值为0,1,4,9,
且有P(ξ=0)=
 ,
,P(ξ=1)=
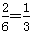 ,
,P(ξ=4)=
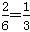 ,
,P(ξ=9)=
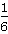
故ξ的分布列为:

所以E(ξ)=
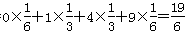 。
。
练习册系列答案
相关题目