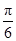题目内容
已知球O是棱长为1的正方体ABCD-A1B1C1D1的外接球,则平面ACD1截球O所得的截面面积为( )
分析:画出图形,求出球心到平面平面ACD1的距离,然后求出截面圆的半径,然后求出截面面积.
解答: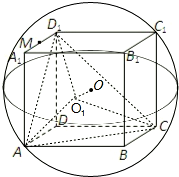 解:如图,由正方体与球的性质可知:球心到平面ACD1的距离为:
解:如图,由正方体与球的性质可知:球心到平面ACD1的距离为:
DB1,
因为正方体的棱长为1,所以
DB1=
,球的半径为:D1O=
.
所以截面圆的半径为:
=
.
所以截面圆的面积为:(
)2π=
π.
故选A.
 解:如图,由正方体与球的性质可知:球心到平面ACD1的距离为:
解:如图,由正方体与球的性质可知:球心到平面ACD1的距离为:| 1 |
| 6 |
因为正方体的棱长为1,所以
| 1 |
| 6 |
| ||
| 6 |
| ||
| 2 |
所以截面圆的半径为:
(
|
|
所以截面圆的面积为:(
|
| 2 |
| 3 |
故选A.
点评:本题考查正方体的外接球与截面面积的求法,考查计算能力,空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
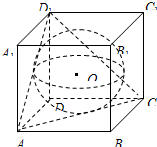 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为
(2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为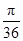 B.
B.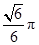 C.
C.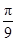 D.
D.