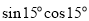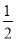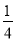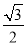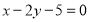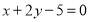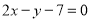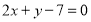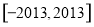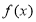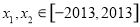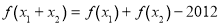题目内容
已知tanα, 是关于x的方程x2-kx+k2-3=0的两实根,且3π<α<
是关于x的方程x2-kx+k2-3=0的两实根,且3π<α<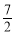 π,
π,
求cos(3π+α)-sin(π+α)的值.
0
【解析】
试题分析:关于方程两根的问题可用韦达定理解决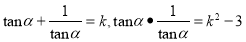 ,,从而求出k =±2,再根据角的范围可知
,,从而求出k =±2,再根据角的范围可知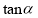 为正,从而求得
为正,从而求得 。根据角的范围可知
。根据角的范围可知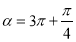 ,利用诱导公式求出sinα=cosα=-
,利用诱导公式求出sinα=cosα=-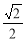 再利用诱导公式求cos(3π+α)和sin(π+α)的值。
再利用诱导公式求cos(3π+α)和sin(π+α)的值。
试题解析:由已知得tanα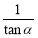 =k2-3=1,∴k=±2.
=k2-3=1,∴k=±2.
又∵3π<α<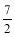 π,∴tanα>0,
π,∴tanα>0,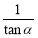 >0.∴tanα+
>0.∴tanα+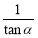 =k=2>0(k=-2舍去),
=k=2>0(k=-2舍去),
∴tanα=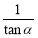 =1,∵3π<α<
=1,∵3π<α<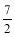 π ∴
π ∴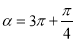
∴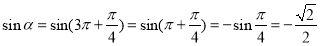 ,
,
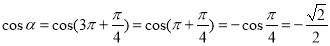
∴cos(3π+α)-sin(π+α)=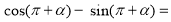 sinα-cosα=0.
sinα-cosα=0.
考点:韦达定理,诱导公式,特殊角的三角函数值

练习册系列答案
相关题目