题目内容
 如图为函数f(x)=
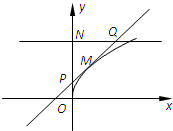
如图为函数f(x)= (0<x<1)的图象,其在点M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为 .
(0<x<1)的图象,其在点M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为 .
【答案】分析:对函数求导可得, ,根据导数的几何意义先写出过点M的切线方程为y-
,根据导数的几何意义先写出过点M的切线方程为y- =
= ,进而可得面积S
,进而可得面积S
= ,令g(t)=
,令g(t)= (0<t<1),要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过
(0<t<1),要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过 =
= 研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解
研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解
解答:解:对函数求导可得,
由题意可得M(t, ),切线的斜率k=
),切线的斜率k=
过点M的切线方程为y- =
=
则可得
 l=
l= l
l
令g(t)= (0<t<1)
(0<t<1)
 =
=
函数g(t)在( )单调递增,在
)单调递增,在 单调递减
单调递减
由于 ,
,
△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点
,根据函数的图象可知

故答案为:
点评:本题主要考查了导数的几何意义的应用:求切线方程;利用导数判断函数的单调性,求解函数的最值,解决本题的关键是构造函数g(t),通过研究该函数的性质,给出相应的函数的图象,从而进行求解
 ,根据导数的几何意义先写出过点M的切线方程为y-
,根据导数的几何意义先写出过点M的切线方程为y- =
= ,进而可得面积S
,进而可得面积S=
 ,令g(t)=
,令g(t)= (0<t<1),要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过
(0<t<1),要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过 =
= 研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解
研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解解答:解:对函数求导可得,

由题意可得M(t,
 ),切线的斜率k=
),切线的斜率k=
过点M的切线方程为y-
 =
=
则可得

 l=
l= l
l令g(t)=
 (0<t<1)
(0<t<1) =
=
函数g(t)在(
 )单调递增,在
)单调递增,在 单调递减
单调递减由于
 ,
,
△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点
,根据函数的图象可知


故答案为:

点评:本题主要考查了导数的几何意义的应用:求切线方程;利用导数判断函数的单调性,求解函数的最值,解决本题的关键是构造函数g(t),通过研究该函数的性质,给出相应的函数的图象,从而进行求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图为函数f(x)=
如图为函数f(x)=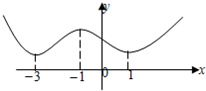
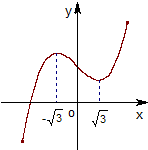 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )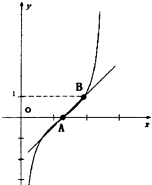 如图为函数f(x)=tan(
如图为函数f(x)=tan(