题目内容
如图有三根针和套在一根针上的n(n∈N*)个金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动1个金属片;
2.较大的金属片不能放在较小的金属片上面.
现用an表示把n个金属片从中间的针移到右边的针上所至少需要移动的次数,请回答下列问题:
(1)写出a1,a2,a3,并求出an;
(2)记bn=an+1,求和Sn=
bibj(i,j∈N*);(其中
bibj表示所有的积bibj(1≤i≤j≤n)的和.例:
bibj=
+b1b2+
=
[(b1+b2)2+(
+
)]
(3)证明:
≤
+
+…+
<
(n∈N*)
1.每次只能移动1个金属片;
2.较大的金属片不能放在较小的金属片上面.
现用an表示把n个金属片从中间的针移到右边的针上所至少需要移动的次数,请回答下列问题:
(1)写出a1,a2,a3,并求出an;
(2)记bn=an+1,求和Sn=
 |
| 1≤i≤j≤n |
 |
| 1≤i≤j≤n |
 |
| 1≤i≤j≤2 |
| b | 2 1 |
| b | 2 2 |
| 1 |
| 2 |
| b | 2 1 |
| b | 2 2 |
(3)证明:
| 1 |
| 7 |
| S1 |
| S2 |
| S1S3 |
| S2S4 |
| S1S3…S2n-1 |
| S2S4…S2n |
| 4 |
| 21 |

分析:(1)由题意要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,需要an-1次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,需要an-1次转移,所以有an=2an-1+1,利用构造法可求an;
(2)由bn=an+1=2n,Sn=
bibj=
[(b1+b2+…+bn)2+(
+
+…+bn2)化简可得Sn=
bibj=
(2n-1)(2n+1-1),再
(3)令cn=
,则当n≥2时,cn<
•
=
•cn-1,从而利用放缩法可证.
(2)由bn=an+1=2n,Sn=
 |
| 1≤i≤j≤n |
| 1 |
| 2 |
| b | 2 1 |
| b | 2 2 |
 |
| 1≤i≤j≤n |
| 4 |
| 3 |
(3)令cn=
| S1S3…S2n-1 |
| S2S4…S2n |
| 1 |
| 4 |
| 1 |
| 22n-1-1 |
| 1 |
| 4 |
解答:解:(1)a1=1,a2=3,a3=7
事实上,要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,需要an-1次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,需要an-1次转移,所以有an=2an-1+1则an+1=2(an-1+1)⇒an+1=2n,所以an=2n-1
(2)bn=an+1=2n
则Sn=
bibj=
[(b1+b2+…+bn)2+(
+
+…+bn2)]=
[(2+22+…+2n)2+(22+24+…+22n)]=
[(2n+1-2)2+
(4n-1)]=
(2n-1)(2n+1-1),
(3)令cn=
,
则当n≥2时cn=
=
•
•…•
=
=
•
<
•
=
•cn-1<(
)n-1c1
又c1=
=
<
∴
+
+…+
<c1+
c1+(
)2c1+…+(
)n-1c1=
•c1=
-
•(
)n<
又∵cn>0恒成立
∴
+
+…+
≥c1=
综上所述:
≤
+
+…+
<
(n∈N*).
事实上,要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,需要an-1次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,需要an-1次转移,所以有an=2an-1+1则an+1=2(an-1+1)⇒an+1=2n,所以an=2n-1
(2)bn=an+1=2n
则Sn=
 |
| 1≤i≤j≤n |
| 1 |
| 2 |
| b | 2 1 |
| b | 2 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
(3)令cn=
| S1S3…S2n-1 |
| S2S4…S2n |
则当n≥2时cn=
| S1S3…S2n-1 |
| S2S4…S2n |
| (21-1)(22-1) |
| (22-1)(23-1) |
| (23-1)(24-1) |
| (24-1)(25-1) |
| (22n-1-1)(22n-1) |
| (22n-1)(22n+1-1) |
=
| 1 |
| 22n+1-1 |
| 1 |
| 4 |
| 1 | ||
22n-1-
|
| 1 |
| 4 |
| 1 |
| 22n-1-1 |
| 1 |
| 4 |
| 1 |
| 4 |
又c1=
| 1 |
| 23-1 |
| 1 |
| 7 |
| 4 |
| 21 |
∴
| S1 |
| S2 |
| S1S3 |
| S2S4 |
| S1S3…S2n-1 |
| S2S4…S2n |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
1-(
| ||
1-
|
| 4 |
| 21 |
| 4 |
| 21 |
| 1 |
| 4 |
| 4 |
| 21 |
又∵cn>0恒成立
∴
| S1 |
| S2 |
| S1S3 |
| S2S4 |
| S1S3…S2n-1 |
| S2S4…S2n |
| 1 |
| 7 |
综上所述:
| 1 |
| 7 |
| S1 |
| S2 |
| S1S3 |
| S2S4 |
| S1S3…S2n-1 |
| S2S4…S2n |
| 4 |
| 21 |
点评:本题的(1)问关键是从特殊中发现一般性的规律,考查构造法求数列的通项;(2)问体现等价转化的数学思想,同时应注意放缩法的运用.

练习册系列答案
相关题目
 (2013•汕尾二模)如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(2013•汕尾二模)如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. 如图所示,有三根针和套在一根针上的n个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
如图所示,有三根针和套在一根针上的n个金属片,按下列规则,把金属片从一根针上全部移到另一根针上. 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上。
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上。
 ,则
,则 =( )
=( )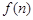 ;则:(Ⅰ)
;则:(Ⅰ)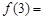 ▲ (Ⅱ)
▲ (Ⅱ) 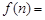 ▲
▲