题目内容
设圆C:(x-5)2+(y-3)2=5,过圆心C作直线l与圆交于A,B两点,与x轴交于P点,若A恰为线段BP的中点,则直线l的方程为( )A.x-3y+4=0,x+3y-14=0
B.2x-y-7=0,2x+y-13=0
C.x-2y+1=0,x+2y-11=0
D.3x-y-12=0,3x+y-18=0
【答案】分析:由题意可设直线l的方程为y-3=k(x-5),P(0,3-5k),设A(x1,y1),B(x2,y2),联立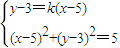 ,然后由方程的根与系数关系可得,x1+x2,x1x2,由A为BP的中点可得x2=2x1,联立可求x1,x2,进而可求k,即可求解直线方程.
,然后由方程的根与系数关系可得,x1+x2,x1x2,由A为BP的中点可得x2=2x1,联立可求x1,x2,进而可求k,即可求解直线方程.
解答:解:∵圆C:(x-5)2+(y-3)2=5,∴C(5,3),
∵过圆心C作直线l与圆交于A,B两点,
∴设直线l的方程为y-3=k(x-5),
令y=0,得x=5-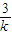 ,即P(5-
,即P(5-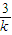 ,0),设A(x1,y1),B(x2,y2)
,0),设A(x1,y1),B(x2,y2)
联立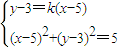 ,消去x可得(1+
,消去x可得(1+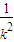 )y2-6(1+
)y2-6(1+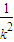 )x+
)x+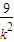 +4=0,
+4=0,
由方程的根与系数关系可得,y1+y2=6,y1y2=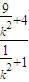 =
=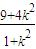 ,①
,①
∵A为BP的中点
∴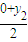 =y1,即y2=2y1,②
=y1,即y2=2y1,②
把②代入①可得y2=4,y1=2,y1y2=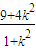 =8,
=8,
∴k=± ,
,
∴直线l的方程为y-3=± (x-5),
(x-5),
即x-2y+1=0,或x+2y-11=0.
故选C.
点评:本题主要考查直线和圆的位置关系,方程的根与系数关系的应用,体现了方程的数学思想,属于中档题.
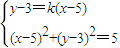 ,然后由方程的根与系数关系可得,x1+x2,x1x2,由A为BP的中点可得x2=2x1,联立可求x1,x2,进而可求k,即可求解直线方程.
,然后由方程的根与系数关系可得,x1+x2,x1x2,由A为BP的中点可得x2=2x1,联立可求x1,x2,进而可求k,即可求解直线方程.解答:解:∵圆C:(x-5)2+(y-3)2=5,∴C(5,3),
∵过圆心C作直线l与圆交于A,B两点,
∴设直线l的方程为y-3=k(x-5),
令y=0,得x=5-
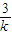 ,即P(5-
,即P(5-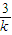 ,0),设A(x1,y1),B(x2,y2)
,0),设A(x1,y1),B(x2,y2)联立
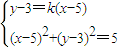 ,消去x可得(1+
,消去x可得(1+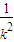 )y2-6(1+
)y2-6(1+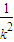 )x+
)x+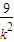 +4=0,
+4=0,由方程的根与系数关系可得,y1+y2=6,y1y2=
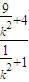 =
=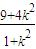 ,①
,①∵A为BP的中点
∴
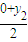 =y1,即y2=2y1,②
=y1,即y2=2y1,②把②代入①可得y2=4,y1=2,y1y2=
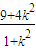 =8,
=8,∴k=±
 ,
,∴直线l的方程为y-3=±
 (x-5),
(x-5),即x-2y+1=0,或x+2y-11=0.
故选C.
点评:本题主要考查直线和圆的位置关系,方程的根与系数关系的应用,体现了方程的数学思想,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目