题目内容
若函数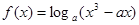
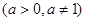 在区间
在区间 内单调递增,则
内单调递增,则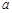 的取值范围是( )
的取值范围是( )
A.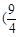 ,
,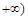 B.(1,
B.(1,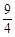 )
C. [
)
C. [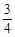 ,1) D. [
,1) D. [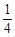 ,1)
,1)
【答案】
C
【解析】当a>1时,根据复合函数的单调性,则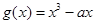 在
在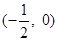 内单调递增,并且
内单调递增,并且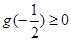 ,
,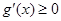 在
在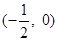 上恒成立,即
上恒成立,即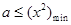 ,因为
,因为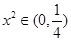 ,显然不成立;当0<a<1时,
,显然不成立;当0<a<1时,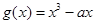 在
在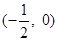 内单减,并且
内单减,并且 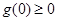 ,
,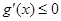 在
在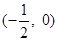 上恒成立,即
上恒成立,即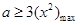 ,因为
,因为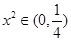 ,所以
,所以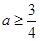 ,所以a的取值范围是
,所以a的取值范围是
[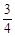 ,1).
,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,(
,( ),
),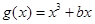
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令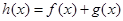 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,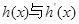 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当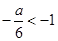 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。



