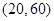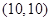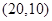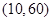题目内容
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式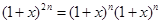 可得,左边
可得,左边 的系数为
的系数为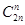 ,
,
而右边 ,
,  的系数为
的系数为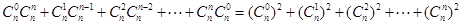 ,
,
由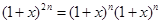 恒成立,可得
恒成立,可得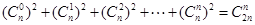 .
.
利用上述方法,化简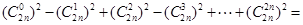 .
.
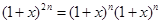 可得,左边
可得,左边 的系数为
的系数为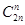 ,
,而右边
 ,
,  的系数为
的系数为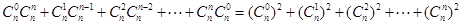 ,
,由
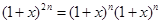 恒成立,可得
恒成立,可得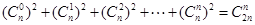 .
.利用上述方法,化简
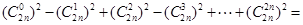 .
.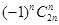
试题分析:构造等式(x-1)2n•(x+1)2n=(x2-1)2n,由左式可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,由右式可得得x2n的系数为(-1)nC2nn,故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
点评:对于此类组合数的应用问题,常常涉及二项式定理的应用,关键要根据题意,充分利用组合数的性质.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
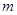 种,选出三人班级委的选法共有
种,选出三人班级委的选法共有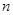 种,则
种,则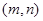 是 ( )
是 ( )