题目内容
设等比数列{![]() }的前
}的前![]() 项和
项和![]() ,首项
,首项![]() ,公比
,公比![]() .
.
(1)证明:![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,
,![]() ,求数列{
,求数列{![]() }的通项公式;
}的通项公式;
(3)若![]() ,记
,记![]() ,数列{
,数列{![]() }的前项和为
}的前项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
解析:(1)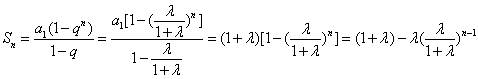
而![]() 所以
所以![]() (2)
(2)![]() ,
,![]() ,
,
![]() 是首项为
是首项为![]() ,公差为1的等差数列,所以
,公差为1的等差数列,所以![]() ,即
,即![]() .
.
(3) ![]() 时,
时,![]() ,
, ![]()
![]()
![]()
相减得![]()
![]() ,
,
又因为![]() ,
,![]() 单调递增,
单调递增, ![]()
故当![]() 时,
时, ![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
设等比数列{![]() }的前
}的前![]() 项和
项和![]() ,首项
,首项![]() ,公比
,公比![]() .
.
(1)证明:![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,
,![]() ,求数列{
,求数列{![]() }的通项公式;
}的通项公式;
(3)若![]() ,记
,记![]() ,数列{
,数列{![]() }的前项和为
}的前项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
解析:(1)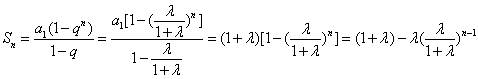
而![]() 所以
所以![]() (2)
(2)![]() ,
,![]() ,
,
![]() 是首项为
是首项为![]() ,公差为1的等差数列,所以
,公差为1的等差数列,所以![]() ,即
,即![]() .
.
(3) ![]() 时,
时,![]() ,
, ![]()
![]()
![]()
相减得![]()
![]() ,
,
又因为![]() ,
,![]() 单调递增,
单调递增, ![]()
故当![]() 时,
时, ![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案