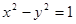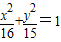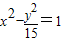题目内容
若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2:1,则称此椭圆或双曲线存在“Ω点”,下列曲线中存在“Ω点”的是( )
分析:验证四个答案中哪一个符合题干中的条件:存在点P,使得点P到两个焦点的距离之比为2:1.
解答:解:若双曲线的方程为x2-y2=1
则双曲线的两个焦点为F1(-
,0)、F2(
,0)
则存在点P(
,
),使得|PF1|:|PF2|=4:2=2:1
即双曲线x2-y2=1存在“Ω点”,
故选C.
则双曲线的两个焦点为F1(-
| 2 |
| 2 |
则存在点P(
3
| ||
| 2 |
| ||
| 2 |
即双曲线x2-y2=1存在“Ω点”,
故选C.
点评:本题考查新定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2:1,则称此椭圆或双曲线存在“F点”,下列曲线中存在“F点”的是( )
A、
| ||||
B、
| ||||
C、x2-
| ||||
| D、x2-y2=1 |
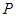 ,使得点
,使得点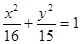 B.
B.
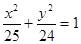
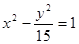 D.
D.