题目内容
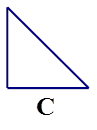
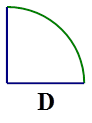
若某空间几何体的三视图如图所示,则该几何体的体积是( )
| A.32 | B.16 | C.24 | D.48 |
B
解析试题分析:
如图,几何体为四棱锥,下底是直角梯形,上底2,下底4,直角腰4, 底面,
底面,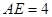 ,
,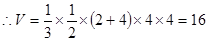 ,故选B.
,故选B.
考点:根据三视图求几何体的体积

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
一空间几何体的三视图如图所示,则该几何体的体积为( )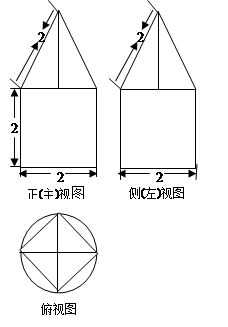
A.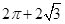 | B.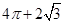 | C.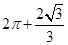 | D.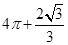 |
若某几何体的三视图如右图所示,则此几何体的体积等于( )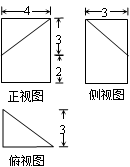
A. | B.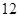 | C.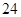 | D.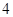 |
两球的体积之比为8:1,则它们的表面积之比为( )
| A.8:1 | B.4:1 | C.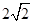 :1 :1 | D.2:1 |
正四棱锥S-ABCD的底面边长为4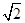 ,高SE=8,则过点A,B,C,D,S的球的半径为( )
,高SE=8,则过点A,B,C,D,S的球的半径为( )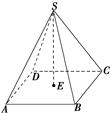
| A.3 | B.4 | C.5 | D.6 |
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为( )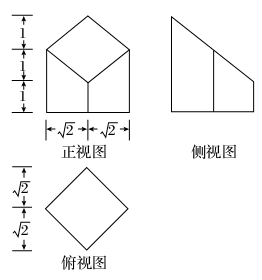
| A.4 | B.2 | C. | D.8 |
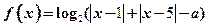 .
. (Ⅰ)当
(Ⅰ)当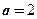 时,求函数
时,求函数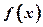 的最小值;
的最小值;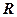 时,求实数
时,求实数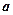 的取值范围。
的取值范围。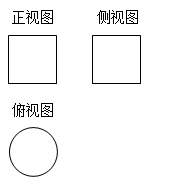
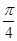
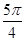
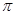

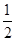 .则该几何体的俯视图可以是( )
.则该几何体的俯视图可以是( )