题目内容
(14分)已知函数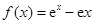 .
.
(Ⅰ)求函数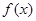 的最小值;
的最小值;
(Ⅱ)求证: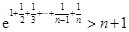
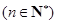 ;
;
(Ⅲ)对于函数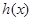 与
与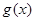 定义域上的任意实数
定义域上的任意实数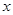 ,若存在常数
,若存在常数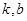 ,使得
,使得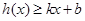 和
和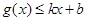 都成立,则称直线
都成立,则称直线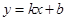 为函数
为函数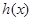 与
与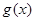 的“分界线”.设函数
的“分界线”.设函数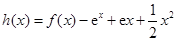 ,
,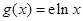 ,
,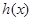 与
与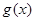 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出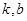 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ) 的最小值为
的最小值为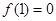 ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)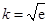 ,
,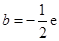
【解析】
试题分析:(Ⅰ)求导得: ,由此可得函数
,由此可得函数 在
在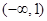 上递减,
上递减,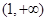 上递增,
上递增,
从而得 的最小值为
的最小值为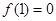 .
.
(Ⅱ)注意用第(Ⅰ)小题的结果.由(Ⅰ)知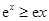 .这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以
.这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以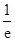 变形为:
变形为: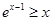 ,把
,把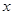 换成
换成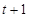 得
得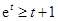 ,在这个不等式中令
,在这个不等式中令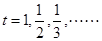 然后将各不等式相乘即得.
然后将各不等式相乘即得.
(Ⅲ)结合题中定义可知,分界线就是一条把两个函数的图象分开的直线.那么如何确定两个函数是否存在分界线?显然,如果两个函数的图象没有公共点,则它们有无数条分界线,如果两个函数至少有两个公共点,则它们没有分界线.所以接下来我们就研究这两个函数是否有公共点.为此设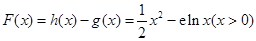 .通过求导可得当
.通过求导可得当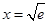 时
时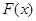 取得最小值0,这说明
取得最小值0,这说明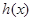 与
与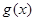 的图象在
的图象在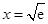 处有公共点
处有公共点 .如果它们存在分界线,则这条分界线必过该点.所以设
.如果它们存在分界线,则这条分界线必过该点.所以设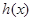 与
与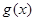 的“分界线”方程为
的“分界线”方程为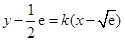 .由于
.由于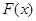 的最小值为0,所以
的最小值为0,所以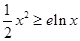 ,所以分界线必满足
,所以分界线必满足 和
和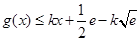 .下面就利用这两个不等式来确定
.下面就利用这两个不等式来确定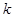 的值.
的值.
试题解析:(Ⅰ)解:因为 ,令
,令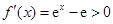 ,解得
,解得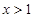 ,
,
令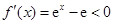 ,解得
,解得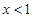 ,
,
所以函数 在
在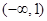 上递减,
上递减,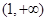 上递增,
上递增,
所以 的最小值为
的最小值为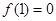 .
3分
.
3分
(Ⅱ)证明:由(Ⅰ)知函数 在
在 取得最小值,所以
取得最小值,所以 ,即
,即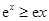
两端同时乘以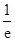 得
得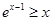 ,把
,把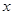 换成
换成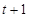 得
得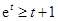 ,当且仅当
,当且仅当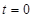 时等号成立.
时等号成立.
由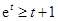 得,
得,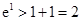 ,
,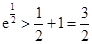 ,
,
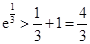 ,
,
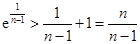 ,
,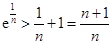 .
.
将上式相乘得
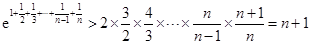 . 9分
. 9分
(Ⅲ)设 .
.
则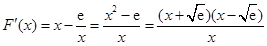 .
.
所以当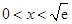 时,
时,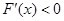 ;当
;当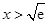 时,
时,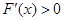 .
.
因此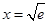 时
时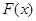 取得最小值0,则
取得最小值0,则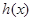 与
与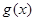 的图象在
的图象在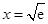 处有公共点
处有公共点 .
.
设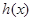 与
与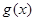 存在
“分界线”,方程为
存在
“分界线”,方程为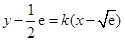 .
.
由 在
在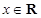 恒成立,
恒成立,
则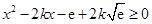 在
在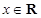 恒成立.
恒成立.
所以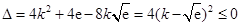 成立.因此
成立.因此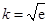 .
.
下面证明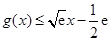
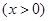 成立.
成立.
设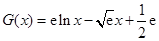 ,
,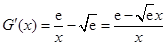 .
.
所以当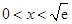 时,
时,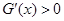 ;当
;当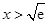 时,
时,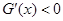 .
.
因此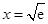 时
时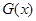 取得最大值0,则
取得最大值0,则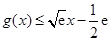
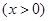 成立.
成立.
所以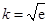 ,
,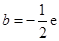 .
14分
.
14分
考点:1、导数的应用;2、函数与不等式;3、新定义概念.

 (
( 为自然对数的底数).
为自然对数的底数). 的最小值;
的最小值; ,证明:
,证明: .
. ,其中
,其中 为自然对数的底数.
为自然对数的底数. 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积; 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为 ,求
,求 的值.
的值. 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 时,
时, ,其中
,其中 .
. 上的解析式,并求出函数
上的解析式,并求出函数 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
). .
. 为
为 的极值点,求实数
的极值点,求实数 的值;
的值; 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围.
的取值范围. (
( ,实数
,实数 ,
, 为常数).
为常数). ,求函数
,求函数 的极值;
的极值; ,讨论函数
,讨论函数