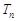题目内容
数列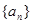 的前n项和为
的前n项和为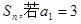 ,
,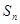 和
和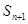 满足等式
满足等式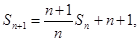
(Ⅰ)求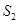 的值;
的值;
(Ⅱ)求证:数列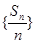 是等差数列;
是等差数列;
(Ⅲ)若数列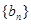 满足
满足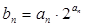 ,求数列
,求数列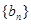 的前n项和
的前n项和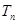 ;
;
(Ⅳ)设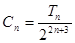 ,求证:
,求证: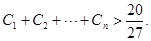
【答案】
(Ⅰ)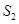 =8 (Ⅱ)见解析(III)
=8 (Ⅱ)见解析(III)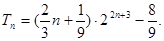 (Ⅳ)见解析
(Ⅳ)见解析
【解析】
试题分析:(Ⅰ)令n=1,代入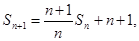 即可; (Ⅱ)利用
即可; (Ⅱ)利用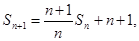 两边同除以n+1,构造等差数列即可; (III)由(II)可知数列
两边同除以n+1,构造等差数列即可; (III)由(II)可知数列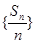 是等差数列,求出
是等差数列,求出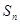 的解析式,再利用
的解析式,再利用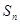 求出
求出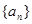 的通项公式
的通项公式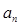 ,代入
,代入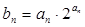 ,求出
,求出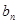 ,再利用错位相减法求出数列
,再利用错位相减法求出数列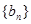 的前n项和
的前n项和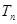 ;(Ⅳ)由(III)知
;(Ⅳ)由(III)知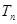 ,代入
,代入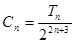 ,求出
,求出 的通项公式,再求出其前n项和,最后利用放缩法得到所求结果.
的通项公式,再求出其前n项和,最后利用放缩法得到所求结果.
试题解析:(Ⅰ)由已知: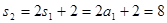
(Ⅱ)∵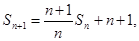 ,同除以n+1,则有:
,同除以n+1,则有: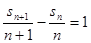 ,所以
,所以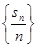 是以3为首项,1为公差的等差数列.
是以3为首项,1为公差的等差数列.
(III)由(II)可知, 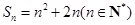

当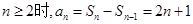 经检验,当n=1时也成立
经检验,当n=1时也成立

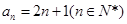
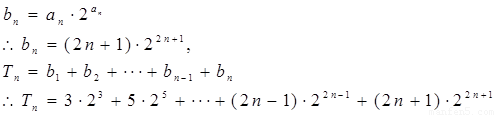
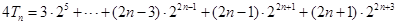
解得: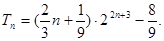
(Ⅳ)∵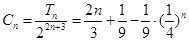
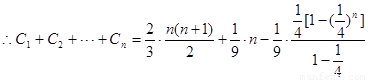

考点:1.等差数列的定义; 2.错位相减法求n前项和;3.放缩法

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,令
,令 ,称
,称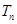 为数列
为数列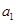 ,
,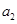 ,……,
,……,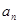 的“平均和”,已知数列
的“平均和”,已知数列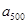 的“平均和”为2004,那么数列2,
的“平均和”为2004,那么数列2, 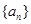 的前n项和为
的前n项和为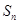 ,
,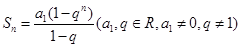
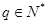 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列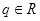 ,是否存在
,是否存在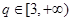 ,使数列
,使数列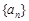 的公比大于1,
的公比大于1,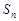 是数列
是数列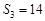 ,且
,且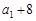 ,
,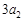 ,
,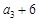 依次成等差数列,数列
依次成等差数列,数列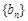 满足:
满足: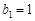 ,
,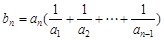
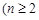 )
)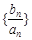 的前n项和为
的前n项和为