Question

（09年长沙一中第八次月考理）(本小题满分12分)如图，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EF//AC,∠CAF=∠AFE=90º,AB=，AF=FE=1.

（1）求证EC//平面BDF；

（2）求二面角A-DF-B的大小；

（3）试在线段AC上确定一点P，使得PF与BC所成的角是60°．

Answer 1

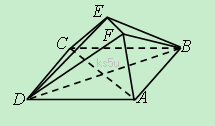
解析： 解法一: (1)记AC与BD的交点为O,连接OF, ∵OC=EF=1 EF//AC∴四边形EFOC是平行四边形，

∴CE∥OF．∵平面BDF，平面BDF，∴CE∥平面BDF．

(2)在平面AFD中过A作AS⊥DF于S，连结BS，∵AB⊥AF， AB⊥AD， ∴AB⊥平面ADF，∴AS是BS在平面ADF上的射影，

由三垂线定理得BS⊥DF．∴∠BSA是二面角A―DF―B的平面角．

在RtΔASB中，

∴∴二面角A―DF―B的大小为60º．

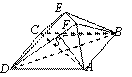
（3）设CP=t（0≤t≤2）,作PQ⊥AB于Q，则PQ∥AD，

∵PQ⊥AB，PQ⊥AF，，∴PQ⊥平面ABF，平面ABF，∴PQ⊥QF．在RtΔPQF中，∠FPQ=60º，PF=2PQ．

∵ΔPAQ为等腰直角三角形，∴又∵ΔPAF为直角三角形，∴，∴所以t=1或t=3(舍去),即点P是AC的中点．

解法二： 空间响亮求解参照计分．