题目内容
设数列{an}为各项均为1的无穷数列,右在此数列的首项a1后面插入一项1,隔两项即a3后面插入一项2,再隔三项即a6后面插入一项3,…,得到这样一个新数列{bn},则数列{bn}的前50项的和为 .
【答案】分析:观察数列{bn},搞清插入的新数组的个数是关键,注意数列{bn}的项数为:2+3+4+5+…+n+1,从而可求.
解答:解:新数列{bn}形如:1 1 1 1 2 1 1 1 3 1 1 1 1 4…
我们可以把Cn:11,112,1113,11114,…组合成新的数组,那么新数组的个数为2、3、4、5…n+1
即数列{bn}的项数为:2+3+4+5+…+n+1
令2+3+4+5+…+n+1=50,∴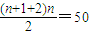 ,∴n(n+3)=100,n=8
,∴n(n+3)=100,n=8
因此数列bn的50项在新数组Cn的第10项的第6个数
数列bn中插入的最大数为9,因此数列{bn}的前50项和为:2+3+…+9+(50-9)=85,故答案为85.
点评:本题考查数列规律的探求,有一定的技巧,属于基础题
解答:解:新数列{bn}形如:1 1 1 1 2 1 1 1 3 1 1 1 1 4…
我们可以把Cn:11,112,1113,11114,…组合成新的数组,那么新数组的个数为2、3、4、5…n+1
即数列{bn}的项数为:2+3+4+5+…+n+1
令2+3+4+5+…+n+1=50,∴
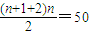 ,∴n(n+3)=100,n=8
,∴n(n+3)=100,n=8因此数列bn的50项在新数组Cn的第10项的第6个数
数列bn中插入的最大数为9,因此数列{bn}的前50项和为:2+3+…+9+(50-9)=85,故答案为85.
点评:本题考查数列规律的探求,有一定的技巧,属于基础题

练习册系列答案
相关题目