题目内容
如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为( )
A. | B.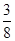 | C. | D. |
A
解析试题分析:一共有2×2×2=8种涂色方法,其中颜色都相同的有2中涂色方法,所以三个形状颜色不全相同的有8-2=6种涂色方法,所以概率为 。
。
考点:排列、组合。
点评:三个颜色不全相同的涂色方法种数较多,我们可以找其对立面即颜色完全相同的情况。应用了正难则反的数学思想。

练习册系列答案
相关题目
把红,黄,蓝,白4张纸牌随机地分发给甲,乙,丙,丁四个人,每人一张,则事件"甲分得红牌"与事件"丁分得红牌"是( )
| A.不可能事件 | B.互斥但不对立事件 | C.对立事件 | D.以上答案都不对 |
设随机变量X~N(0,1),已知 ,则
,则 ( )
( )
| A.0.025 | B.0.050 |
| C.0.950 | D.0.975 |
已知 是
是 所在平面内一点,
所在平面内一点, ,现将一粒
,现将一粒
黄豆随机撒在 内,则黄豆落在
内,则黄豆落在 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
先后抛掷两颗骰子,设出现的点数之和是10,11,12的概率依次是P1,P2,P3,则( )
| A.P1>P2>P3 | B.P1>P2=P3 | C.P1=P2>P3 | D.P1=P2<P3 |
在商场付款处排队等候付款的人数及其概率如下:
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
A.0.9 B. 0.74 C. 0.56 D.0.26





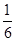


 的面积大于
的面积大于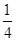 的概率是( )
的概率是( )

