题目内容
设双曲线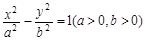 的离心率为
的离心率为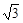 ,且它的一条准线与抛物线
,且它的一条准线与抛物线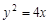 的准线重合,则此双曲线的方程为
的准线重合,则此双曲线的方程为
A.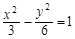 | B.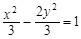 | C.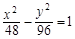 | D.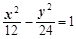 |
A
解析

练习册系列答案
相关题目
已知双曲线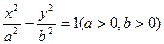 的右焦点为F,若过点且斜率为
的右焦点为F,若过点且斜率为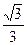 的直线
的直线
与双曲线渐近线平行,则此双曲线离心率是 ( )
A.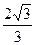 | B.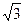 | C.2 | D.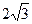 |
如图,用与底面成30°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A.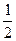 | B.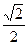 |
C.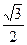 | D.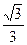 |
过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
方程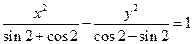 所表示的轨迹是焦点在( )
所表示的轨迹是焦点在( )
A.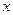 轴上的椭圆 轴上的椭圆 | B.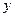 轴上的椭圆 轴上的椭圆 |
C.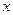 轴上的双曲线 轴上的双曲线 | D.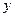 轴上的双曲线 轴上的双曲线 |
抛物线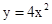 上的一点M到焦点的距离为1,则点M的纵坐标为( )
上的一点M到焦点的距离为1,则点M的纵坐标为( )
A.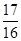 | B.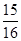 | C.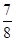 | D.0 |
椭圆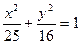 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若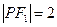 ,则
,则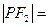
| A.2 | B.4 | C.6 | D.8 |
设A是椭圆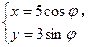 (
(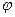 是参数)的左焦点,P是椭圆上对应于
是参数)的左焦点,P是椭圆上对应于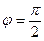 的点,那么线段AP的长是
的点,那么线段AP的长是
| A.1 | B.5 | C.7 | D.10 |
已知抛物线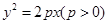 ,过点
,过点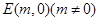 的直线交抛物线于点M、N,交y轴于点P,若
的直线交抛物线于点M、N,交y轴于点P,若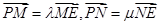 ,则
,则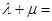 ( )
( )
| A.1 | B.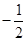 | C.-1 | D.-2 |