题目内容
已知两点M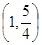 ,N
,N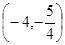 ,给出下列曲线方程:①
,给出下列曲线方程:①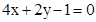 ;②
;②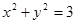 ;
;
③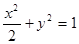 ;④
;④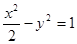 。在曲线上存在点P满足
。在曲线上存在点P满足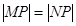 的所有曲线方程是( )
的所有曲线方程是( )
A. ①②③④ B. ①③ C. ②④ D.②③④
【答案】
D
【解析】解:要使这些曲线上存在点P满足|MP|=|NP|,需曲线与MN的垂直平分线相交.根据M,N的坐标求得MN垂直平分线的方程,分别于题设中的方程联立,看有无交点即可
∵①4x+2y-1=0与y=-2(x+3/2),斜率相同,两直线平行,可知两直线无交点,进而可知①不符合题意.
②x2+y2=3与y=-2(x+3/2),联立,消去y得5x2-12x+6=0,△=144-4×5×6>0,可知②中的曲线与MN的垂直平分线有交点,③中的方程与y=-2(x+3/2),联立,消去y得9x2-24x-16=0,△>0可知③中的曲线与MN的垂直平分线有交点,
④中的方程与y=-2(x+3/2),联立,消去y得7x2-24x+20=0,△>0可知④中的曲线与MN的垂直平分线有交点,同理

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 ,N
,N ,给出下列曲线方程:①
,给出下列曲线方程:① ;②
;② ;
; ;④
;④ 。在曲线上存在点P满足
。在曲线上存在点P满足 的所有曲线方程是( )
的所有曲线方程是( ) ,N
,N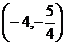 ,给出下列曲线方程:①
,给出下列曲线方程:①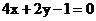 ;②
;②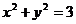 ;
;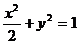 ;④
;④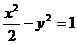 。在曲线上存在点P满足
。在曲线上存在点P满足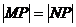 的所有曲线方程是( )
的所有曲线方程是( )