题目内容
椭圆的对称中心在坐标原点,一个顶点为A(0,2),右焦点F与点B(| 2 |
| 2 |
(1)求椭圆的方程;
(2)是否存在斜率k≠0的直线l:y=kx-2,使直线l与椭圆相交于不同的两点M,N满足|
| AM |
| AN |
分析:(1)设出椭圆的标准方程,由题意得b=2,再由a、b、c之间的关系及|FB|=2,求出a2=12,从而得到椭圆的方程.
(2)假设存在直线l,则点A在线段MN的垂直平分线上,把直线l的方程代入椭圆的方程,转化为关于x的一元二次方程,由题意知判别式大于0,设出M、N的坐标,利用一元二次方程根与系数的关系,用斜率表示MN的中点P的坐标,求出AP的斜率,由AP⊥MN,斜率之积等于-1,求出直线l的斜率,进而得到直线的倾斜角.
(2)假设存在直线l,则点A在线段MN的垂直平分线上,把直线l的方程代入椭圆的方程,转化为关于x的一元二次方程,由题意知判别式大于0,设出M、N的坐标,利用一元二次方程根与系数的关系,用斜率表示MN的中点P的坐标,求出AP的斜率,由AP⊥MN,斜率之积等于-1,求出直线l的斜率,进而得到直线的倾斜角.
解答:解:(1)依题意,设椭圆方程为
+
=1 ( a>b>0 ),
则其右焦点坐标为F(c , 0 ) ,c=
,(1分)
由|FB|=2,得
=2,
即(c-
)2+2=4,解得c=2
.(3分)
又∵b=2,∴a2=c2+b2=12,即椭圆方程为
+
=1.(4分)
(2)由|AM|=|AN|知点A在线段MN的垂直平分线上,
由
消去y得x2+3(kx-2)2=12
即(1+3k2)x2-12kx=0(6分)
由k≠0,得方程的△=(-12k)2=144k2>0,即方程有两个不相等的实数根. (7分)
设M(x1,y1)、N(x2,y2),线段MN的中点P(x0,y0),
则x1+x2=
,∴x0=
=
,
∴y0=kx0-2=
=
,即P (
,
),(9分)
∵k≠0,∴直线AP的斜率为k1=
=
,(10分)
由AP⊥MN,得
×k=-1,(11分)
∴2+2+6k2=6,解得:k=±
,即tanα=±
,(12分)
又0≤α<π,故α=
,或α=
,
∴存在直线l满足题意,其倾斜角α=
,或α=
.(13分)
| x2 |
| a2 |
| y2 |
| b2 |
则其右焦点坐标为F(c , 0 ) ,c=
| a2-b2 |
由|FB|=2,得
(c-
|
即(c-
| 2 |
| 2 |
又∵b=2,∴a2=c2+b2=12,即椭圆方程为
| x2 |
| 12 |
| y2 |
| 4 |
(2)由|AM|=|AN|知点A在线段MN的垂直平分线上,
由
|
即(1+3k2)x2-12kx=0(6分)
由k≠0,得方程的△=(-12k)2=144k2>0,即方程有两个不相等的实数根. (7分)
设M(x1,y1)、N(x2,y2),线段MN的中点P(x0,y0),
则x1+x2=
| 12k |
| 1+3k2 |
| x1+x2 |
| 2 |
| 6k |
| 1+3k2 |
∴y0=kx0-2=
| 6k2-2 (1+3k2) |
| 1+3k2 |
| -2 |
| 1+3k2 |
| 6k |
| 1+3k2 |
| -2 |
| 1+3k2 |
∵k≠0,∴直线AP的斜率为k1=
| ||
|
| -2-2(1+3k2) |
| 6k |
由AP⊥MN,得
| -2-2(1+3k2) |
| 6k |
∴2+2+6k2=6,解得:k=±
| ||
| 3 |
| ||
| 3 |
又0≤α<π,故α=
| π |
| 6 |
| 5π |
| 6 |
∴存在直线l满足题意,其倾斜角α=
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查用待定系数法求椭圆的标注方程,直线与圆锥曲线的位置关系,一元二次方程根与系数的关系,两直线垂直的性质,
以及直线的倾斜角与斜率的关系.
以及直线的倾斜角与斜率的关系.

练习册系列答案
相关题目
 的距离为2.
的距离为2. ,若存在,求直线l的倾斜角α;若不存在,说明理由.
,若存在,求直线l的倾斜角α;若不存在,说明理由.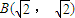 的距离为2.
的距离为2.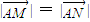 ,若存在,求直线l的倾斜角α;若不存在,说明理由.
,若存在,求直线l的倾斜角α;若不存在,说明理由.