题目内容
已知P:对任意a∈[1,2],不等式|m-5|≤| a2+8 |
分析:若P真,则2≤m≤8;若q真,则1<m<3.由p 或q为真,p且q假,知p假q真或p真q假.若p假q真,则1<m<2.若p真q假,则3≤m≤8.由此能得到实数m的取值范围.
解答:解:若P真,则2≤m≤8;若q真,则1<m<3.
∵p 或q为真,p且q假,
∴p假q真或p真q假.
(1)若p假q真,则m<2或m>8,且1<m<3,
∴1<m<2.
(2)若p真q假,则2≤m≤8,m≤1或m≥3,
∴3≤m≤8.
综上所述:m∈(1,2)∪[3,8]
∵p 或q为真,p且q假,
∴p假q真或p真q假.
(1)若p假q真,则m<2或m>8,且1<m<3,
∴1<m<2.
(2)若p真q假,则2≤m≤8,m≤1或m≥3,
∴3≤m≤8.
综上所述:m∈(1,2)∪[3,8]
点评:本题考查命的真假判断和应用,解题时要认真审题,仔细解答.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
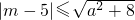 恒成立;q:方程4x2+4(m-2)x+1=0无实根,若p 或q为真,p且q假,求实数m的取值范围.
恒成立;q:方程4x2+4(m-2)x+1=0无实根,若p 或q为真,p且q假,求实数m的取值范围.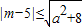 恒成立;q:方程4x2+4(m-2)x+1=0无实根,若p 或q为真,p且q假,求实数m的取值范围.
恒成立;q:方程4x2+4(m-2)x+1=0无实根,若p 或q为真,p且q假,求实数m的取值范围.