题目内容
某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为x元/本(9≤x≤11),预计一年的销售量为(20-x)2万本.(1)求该出版社一年的利润L(万元)与每本书的定价x的函数关系式;
(2)当每本书的定价为多少元时,该出版社一年的利润L最大,并求出L的最大值R(m).
【答案】分析:(1)该出版社一年的利润L(万元)为每本书的利润与一年的销售量的积,故可得函数解析式;
(2)求导函数,确定导数的符号,进而分类讨论确定函数的最值.
解答:解:(1)该出版社一年的利润L(万元)与每本书定价x的函数关系式为:L=(x-5-m)(20-x)2,x∈[9,11].…(4分)
(2)求导函数可得L′(x)=(20-x)(30+2m-3x).…(6分)
令L′=0得x=10+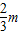 或x=20(不合题意,舍去).…(7分)
或x=20(不合题意,舍去).…(7分)
∵1≤m≤3,∴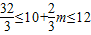 .
.
在x=10+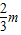 两侧L′的值由正变负.
两侧L′的值由正变负.
所以①当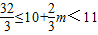 ,即1≤m<
,即1≤m< 时,Lmax=L(10+
时,Lmax=L(10+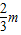 )=4(5-
)=4(5-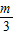 )3.…(9分)
)3.…(9分)
②当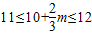 ,即
,即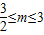 时,Lmax=L(11)=81(6-m),…(11分)
时,Lmax=L(11)=81(6-m),…(11分)
所以R(m)=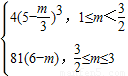
答:若1≤m< ,则当每本书定价为10+
,则当每本书定价为10+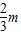 元时,出版社一年的利润L最大,最大值R(m)=4(5-
元时,出版社一年的利润L最大,最大值R(m)=4(5-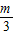 )3(万元);若
)3(万元);若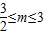 ,则当每本书定价为11元时,出版社一年的利润L最大,最大值R(m)=81(6-m)(万元).…(14分)
,则当每本书定价为11元时,出版社一年的利润L最大,最大值R(m)=81(6-m)(万元).…(14分)
点评:本题考查函数模型的构建,考查导数知识的运用,解题的关键是确定函数的模型,属于中档题.
(2)求导函数,确定导数的符号,进而分类讨论确定函数的最值.
解答:解:(1)该出版社一年的利润L(万元)与每本书定价x的函数关系式为:L=(x-5-m)(20-x)2,x∈[9,11].…(4分)
(2)求导函数可得L′(x)=(20-x)(30+2m-3x).…(6分)
令L′=0得x=10+
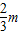 或x=20(不合题意,舍去).…(7分)
或x=20(不合题意,舍去).…(7分)∵1≤m≤3,∴
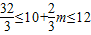 .
.在x=10+
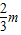 两侧L′的值由正变负.
两侧L′的值由正变负.所以①当
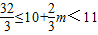 ,即1≤m<
,即1≤m< 时,Lmax=L(10+
时,Lmax=L(10+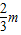 )=4(5-
)=4(5-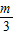 )3.…(9分)
)3.…(9分)②当
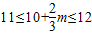 ,即
,即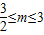 时,Lmax=L(11)=81(6-m),…(11分)
时,Lmax=L(11)=81(6-m),…(11分)所以R(m)=
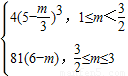
答:若1≤m<
 ,则当每本书定价为10+
,则当每本书定价为10+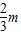 元时,出版社一年的利润L最大,最大值R(m)=4(5-
元时,出版社一年的利润L最大,最大值R(m)=4(5-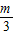 )3(万元);若
)3(万元);若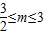 ,则当每本书定价为11元时,出版社一年的利润L最大,最大值R(m)=81(6-m)(万元).…(14分)
,则当每本书定价为11元时,出版社一年的利润L最大,最大值R(m)=81(6-m)(万元).…(14分)点评:本题考查函数模型的构建,考查导数知识的运用,解题的关键是确定函数的模型,属于中档题.

练习册系列答案
相关题目
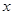 元/本(9≤
元/本(9≤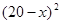 万本.
万本.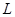 (万元)与每本书的定价
(万元)与每本书的定价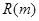 .
.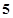 元一本,经销过程中每本书需付给代理商
元一本,经销过程中每本书需付给代理商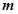 元
元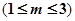 的劳务费,经出版社研究决定,新书投放市场后定价为
的劳务费,经出版社研究决定,新书投放市场后定价为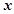 元一本,
元一本,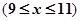 ,预计一年的销售量为
,预计一年的销售量为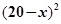 万本.
万本. (万元)与每本书的定价
(万元)与每本书的定价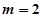 时,当每本书的定价为多少元时,该出版社一年利润
时,当每本书的定价为多少元时,该出版社一年利润