题目内容
已知函数f(x)=(2-a)(x-1)-21nx,g(x)=xe1-x.(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,![]() )上无零点,求a的最小值;
)上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
答案:
解析:
解析:
|
解:(Ⅰ)当 由 故 (Ⅱ)因为 故要使函数 只要对任意的 即对 令 则 综上,若函数 (Ⅲ) 所以,函数 故 此时,当
即②对任意 由③式解得: 综合①④可知,当 在 使 |

练习册系列答案
相关题目
 7分
7分


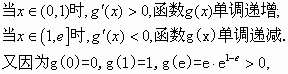
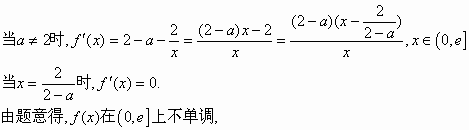


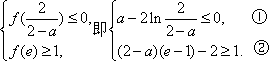
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有