题目内容
已知函数是奇函数,并且函数 的图像经过点
的图像经过点 ,
,
(1)求实数 的值;
的值;
(2)求函数 的值域;
的值域;
(3)证明函数 在(0,+
在(0,+ 上单调递减,并写出
上单调递减,并写出 的单调区间.
的单调区间.
 的图像经过点
的图像经过点 ,
,(1)求实数
 的值;
的值; (2)求函数
 的值域;
的值域;(3)证明函数
 在(0,+
在(0,+ 上单调递减,并写出
上单调递减,并写出 的单调区间.
的单调区间.解:⑴法一:由题意得
解得 .经检验
.经检验 为奇函数
为奇函数
法二 是奇函数,
是奇函数, ,即
,即
 ,得
,得 ,
,
所以 ,得
,得 ,
,
又 ,所以
,所以 ,即
,即
所以 .
.
(2)法一: =
= ,
,
 ∴
∴ ∴
∴ ∴
∴
∴
法二:由 得
得
 ∴
∴ 解得
解得
∴
⑶
…………
 >0
>0
∴函数 在(0,+
在(0,+ 上单调递减
上单调递减
∵函数 是奇函数,∴
是奇函数,∴ 在(-∞,0)上也是递减
在(-∞,0)上也是递减
∴
 的单调减区间为(-∞,0),(0,+
的单调减区间为(-∞,0),(0,+

解得
 .经检验
.经检验 为奇函数
为奇函数法二
 是奇函数,
是奇函数, ,即
,即 ,得
,得 ,
,所以
 ,得
,得 ,
, 又
 ,所以
,所以 ,即
,即
所以
 .
. (2)法一:
 =
= ,
, ∴
∴ ∴
∴ ∴
∴
∴

法二:由
 得
得
 ∴
∴ 解得
解得
∴

⑶

…………
 >0
>0∴函数
 在(0,+
在(0,+ 上单调递减
上单调递减∵函数
 是奇函数,∴
是奇函数,∴ 在(-∞,0)上也是递减
在(-∞,0)上也是递减∴

 的单调减区间为(-∞,0),(0,+
的单调减区间为(-∞,0),(0,+
略

练习册系列答案
相关题目
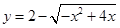 的值域是 ▲
的值域是 ▲ 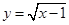 的定义域为( )
的定义域为( )



 ,
, 的值域.
的值域. 的定义域是 ( )
的定义域是 ( ) 



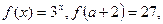 函数
函数
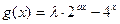 的定义域为[0,2]
的定义域为[0,2]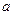 的值
的值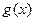 的最大值是
的最大值是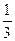 ,求实数
,求实数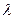 的值。
的值。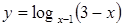 的定义域是
的定义域是 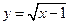 的定义域为
的定义域为  ,则
,则