题目内容
设0<| |≤2,函数f(x)=cos2x-|
|≤2,函数f(x)=cos2x-| |sinx-|
|sinx-| |的最大值0,最小值为-4,且
|的最大值0,最小值为-4,且 与
与 的夹角为45°,求(
的夹角为45°,求( +
+ )2.
)2.
解:f(x)=cos2x-| |sinx-|
|sinx-| |=-sin2x-|
|=-sin2x-| |sinx-|
|sinx-| |+1=-
|+1=- +
+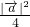 -|
-| |+1,
|+1,
因为-1≤sinx≤1,0<| |≤2?-1<-
|≤2?-1<-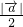 <0,
<0,
所以当sinx=-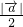 时,f(x)取得最大值为
时,f(x)取得最大值为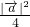 -|
-| |+1,
|+1,
当sinx=1时,f(x)取得最小值为-| |-|
|-| |,
|,
由题意得,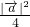 -|
-| |+1=0①,-|
|+1=0①,-| |-|
|-| |=-4②,
|=-4②,
联立①②解得| |=2,|
|=2,| |=2,
|=2,
又 与
与 的夹角为45°,
的夹角为45°,
所以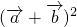 =
= =4+4+2×2×2cos45°=8+4
=4+4+2×2×2cos45°=8+4 .
.
分析:由已知f(x)可变形为:f(x)=- +
+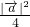 -|
-| |+1,根据-1≤sinx≤1,0<|
|+1,根据-1≤sinx≤1,0<| |≤2及二次函数性质可求出f(x)的最大值、最小值,令其分别为0,-4,可解出|
|≤2及二次函数性质可求出f(x)的最大值、最小值,令其分别为0,-4,可解出| |,|
|,| |,进而可求得
|,进而可求得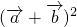 .
.
点评:本题考查二次函数在闭区间上的最值求解及向量的数量积运算,考查学生综合运用知识解决问题的能力,属中档题.
 |sinx-|
|sinx-| |=-sin2x-|
|=-sin2x-| |sinx-|
|sinx-| |+1=-
|+1=- +
+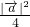 -|
-| |+1,
|+1,因为-1≤sinx≤1,0<|
 |≤2?-1<-
|≤2?-1<-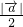 <0,
<0,所以当sinx=-
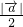 时,f(x)取得最大值为
时,f(x)取得最大值为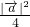 -|
-| |+1,
|+1,当sinx=1时,f(x)取得最小值为-|
 |-|
|-| |,
|,由题意得,
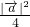 -|
-| |+1=0①,-|
|+1=0①,-| |-|
|-| |=-4②,
|=-4②,联立①②解得|
 |=2,|
|=2,| |=2,
|=2,又
 与
与 的夹角为45°,
的夹角为45°,所以
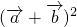 =
= =4+4+2×2×2cos45°=8+4
=4+4+2×2×2cos45°=8+4 .
.分析:由已知f(x)可变形为:f(x)=-
 +
+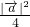 -|
-| |+1,根据-1≤sinx≤1,0<|
|+1,根据-1≤sinx≤1,0<| |≤2及二次函数性质可求出f(x)的最大值、最小值,令其分别为0,-4,可解出|
|≤2及二次函数性质可求出f(x)的最大值、最小值,令其分别为0,-4,可解出| |,|
|,| |,进而可求得
|,进而可求得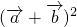 .
.点评:本题考查二次函数在闭区间上的最值求解及向量的数量积运算,考查学生综合运用知识解决问题的能力,属中档题.

练习册系列答案
相关题目