题目内容
已知点P为双曲线 右支上一点,F1,F2为双曲线的左、右焦点.O为坐标原点,若
右支上一点,F1,F2为双曲线的左、右焦点.O为坐标原点,若 且△PF1F2的面积为2ac(c为双曲线半焦距)则双曲线的离心率为 .
且△PF1F2的面积为2ac(c为双曲线半焦距)则双曲线的离心率为 .
【答案】分析:根据向量数量积的运算性质,可得| |=
|= |
|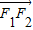 |,得△PF1F2是以P为直角顶点的直角三角形.由双曲线的定义结合勾股定理,算出S△PF1F2=c2-a2=2ac,将其转化为关于离心率e的方程,解之即可得到该双曲线的离心率.
|,得△PF1F2是以P为直角顶点的直角三角形.由双曲线的定义结合勾股定理,算出S△PF1F2=c2-a2=2ac,将其转化为关于离心率e的方程,解之即可得到该双曲线的离心率.
解答:解:∵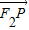 =
=
∴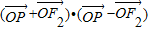 =
=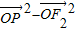 =0
=0
可得|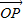 |=|
|=|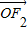 |=
|= |
|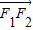 |,所以△PF1F2是以P为直角顶点的直角三角形
|,所以△PF1F2是以P为直角顶点的直角三角形
∵| |-|
|-|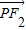 |=±2a
|=±2a
∴(|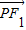 |-|
|-|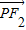 |)2=|
|)2=|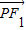 |2-2|
|2-2|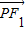 |•|
|•| |+|
|+|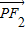 |2=4a2
|2=4a2
∵|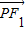 |2+|
|2+| |2=4c2,|
|2=4c2,|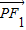 |•|
|•| |=2S△PF1F2,
|=2S△PF1F2,
∴4c2-4S△PF1F2=4a2,得S△PF1F2=c2-a2
∵由题意△PF1F2的面积为2ac,
∴c2-a2=2ac,两边都除以a2,得 -1=2•
-1=2•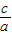
整理,得e2-2e-1=0,解之得e=1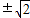 (舍负)
(舍负)
故答案为:1+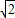
点评:本题给出双曲线的焦点三角是直角三角形,求该双曲线的离心率,着重考查了双曲线的简单几何性质、双曲线的离心率定义及其求法等知识,属于中档题.
 |=
|= |
|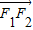 |,得△PF1F2是以P为直角顶点的直角三角形.由双曲线的定义结合勾股定理,算出S△PF1F2=c2-a2=2ac,将其转化为关于离心率e的方程,解之即可得到该双曲线的离心率.
|,得△PF1F2是以P为直角顶点的直角三角形.由双曲线的定义结合勾股定理,算出S△PF1F2=c2-a2=2ac,将其转化为关于离心率e的方程,解之即可得到该双曲线的离心率.解答:解:∵
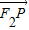 =
=
∴
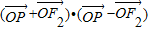 =
=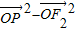 =0
=0可得|
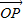 |=|
|=|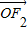 |=
|= |
|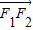 |,所以△PF1F2是以P为直角顶点的直角三角形
|,所以△PF1F2是以P为直角顶点的直角三角形∵|
 |-|
|-|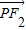 |=±2a
|=±2a∴(|
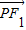 |-|
|-|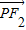 |)2=|
|)2=|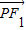 |2-2|
|2-2|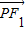 |•|
|•| |+|
|+|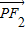 |2=4a2
|2=4a2∵|
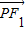 |2+|
|2+| |2=4c2,|
|2=4c2,|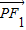 |•|
|•| |=2S△PF1F2,
|=2S△PF1F2,∴4c2-4S△PF1F2=4a2,得S△PF1F2=c2-a2
∵由题意△PF1F2的面积为2ac,
∴c2-a2=2ac,两边都除以a2,得
 -1=2•
-1=2•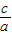
整理,得e2-2e-1=0,解之得e=1
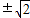 (舍负)
(舍负)故答案为:1+
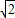
点评:本题给出双曲线的焦点三角是直角三角形,求该双曲线的离心率,着重考查了双曲线的简单几何性质、双曲线的离心率定义及其求法等知识,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 右支上一点,F1、F2分别为双曲线的左、右焦点,I为
右支上一点,F1、F2分别为双曲线的左、右焦点,I为 的内心,若
的内心,若 成立,则
成立,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.
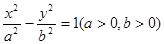 右支上一点,
右支上一点,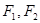 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且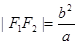 ,I为三角形
,I为三角形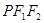 的内心,若
的内心,若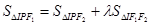 成立,则
成立,则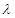 的值为( )
的值为( )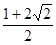 B.
B.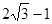 C.
C.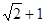 D.
D.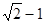
 右支上一点,F1、F2分别为双曲线的左、右焦点,I为△PF1F2的内心,若
右支上一点,F1、F2分别为双曲线的左、右焦点,I为△PF1F2的内心,若 成立,则λ的值为( )
成立,则λ的值为( )



 右支上一点,F1,F2为双曲线的左、右焦点.O为坐标原点,若
右支上一点,F1,F2为双曲线的左、右焦点.O为坐标原点,若 且△PF1F2的面积为2ac(c为双曲线半焦距)则双曲线的离心率为 .
且△PF1F2的面积为2ac(c为双曲线半焦距)则双曲线的离心率为 .