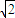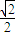题目内容
设E,F,G分别是正四面体ABCD的棱AB,BC,CD的中点,则二面角C-FG-E的大小是( )
A.arcsin
| B.
| ||||||||||
C.
| D.π-arccot
|
取EG中点N,FG中点M,连接MN,CM
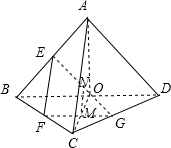
因为FG∥BD,EF∥AC,AC⊥BD,所以EF⊥FG,所以MN⊥FG
因为CM⊥FG,所以∠CMN即为所求二面角.
因为MN∥AC,所以∠CMN=180-∠ACM
取BD中点O,连接OA,OC
在△OAC中,设AC=1,则OA=OC=
所以cos∠ACO=
=
所以cot∠ACO=
所以∠CMN=π-arccot
故选D.

因为FG∥BD,EF∥AC,AC⊥BD,所以EF⊥FG,所以MN⊥FG
因为CM⊥FG,所以∠CMN即为所求二面角.
因为MN∥AC,所以∠CMN=180-∠ACM
取BD中点O,连接OA,OC
在△OAC中,设AC=1,则OA=OC=
| ||
| 2 |
所以cos∠ACO=
| AC2+CO2-AO2 |
| 2AC×CO |
| ||
| 3 |
所以cot∠ACO=
| ||
| 2 |
所以∠CMN=π-arccot
| ||
| 2 |
故选D.

练习册系列答案
相关题目
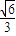
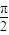 +arccos
+arccos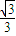
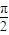 -arctan
-arctan