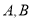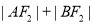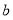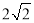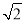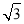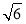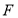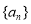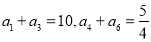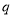题目内容
设数列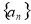 的前
的前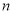 项和为
项和为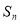 ,
,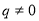 ,
,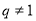 .证明:数列
.证明:数列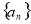 是公比为
是公比为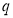 的等比数列的充要条件是
的等比数列的充要条件是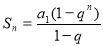 .
.
证明见解析
【解析】
试题分析:要解决这个问题,首先要分清楚必要性和充分性.
由数列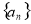 的前
的前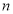 项和为
项和为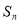 ,
, ,
,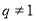 ,数列
,数列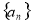 是公比为
是公比为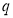 的等比数列
的等比数列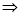
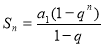 .
.
说明:“数列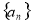 是公比为
是公比为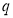 的等比数列”的必要条件是:“
的等比数列”的必要条件是:“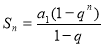 ”
”
由“数列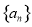 的前
的前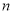 项和
项和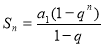 ”
”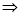 “数列
“数列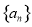 是等比数列”
是等比数列”
说明“数列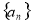 是公比为
是公比为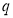 的等比数列”的充分条件是:“
的等比数列”的充分条件是:“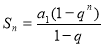 ”
”
前者其实就是等比数列前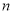 项和公式推导过程的一部分;后者由
项和公式推导过程的一部分;后者由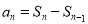 求出
求出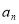 的表达式 ,再紧扣等比数列的定义得出结论.
的表达式 ,再紧扣等比数列的定义得出结论.
试题解析:证明:(1)必要性:
∵数列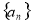 是公比为
是公比为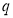 的等比数列
的等比数列
∴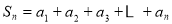
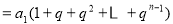 ① 2分
① 2分
①式两边同乘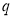 ,得
,得
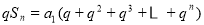 ② 4分
② 4分
①-②,得
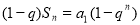 6分
6分
∵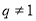
∴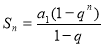 7分
7分
(2)充分性:
由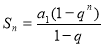 ,得
,得 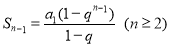 8分
8分
∴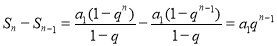
即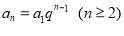 10分
10分
∵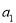 也适合上式
也适合上式
∴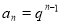 12分
12分
∵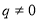
∴当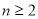 时,
时,
∴数列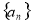 是公比为
是公比为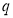 的等比数列 14分
的等比数列 14分
考点:1、充要条件的概念;2、等比数列的定义;3、在数列中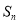 与
与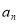 的关系.
的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目