题目内容
12.计算:(1)${({\frac{1}{125}})^{-\frac{2}{3}}}×{5^{-1}}÷{({\frac{1}{16}})^{\frac{1}{4}}}$;
(2)$\frac{1}{2}$lg$\frac{32}{9}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{45}$.
分析 (1)直接利用有理指数幂以及根式运算法则求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)${({\frac{1}{125}})^{-\frac{2}{3}}}×{5^{-1}}÷{({\frac{1}{16}})^{\frac{1}{4}}}$
=${(\frac{1}{5})}^{-2}×{5}^{-1}÷{(\frac{1}{2})}^{4×\frac{1}{4}}$
=5÷$\frac{1}{2}$
=10.
(2)$\frac{1}{2}$lg$\frac{32}{9}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{45}$
=$\frac{5}{2}lg2-lg3-2lg2+\frac{1}{2}lg9+\frac{1}{2}lg5$
=$\frac{1}{2}lg2+\frac{1}{2}lg5$
=$\frac{1}{2}$.
点评 本题考查对数运算法则的应用,有理指数幂的化简求值,是基础题.

练习册系列答案
相关题目
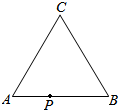 (2015年1月•丰台期末•16)如图.某机器人的运动轨道是边长为1米的正三角形ABC.开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变-次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2.x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2.机器人到A点的距离d与x满足函数关系d=f(x).现有如下结论:
(2015年1月•丰台期末•16)如图.某机器人的运动轨道是边长为1米的正三角形ABC.开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变-次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2.x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2.机器人到A点的距离d与x满足函数关系d=f(x).现有如下结论: