题目内容
如图,设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°.求: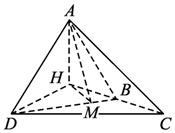
(1)A、D的连线和平面BCD所成的角;
(2)A、D的连线和直线BC所成的角;
(3)二面角A—BD—C的大小.(用反三角函数表示)
解:(1)作AH⊥BC交CB延长线于点H,连结HD.
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AH![]() 平面ABC,AH⊥BC,
平面ABC,AH⊥BC,
∴AH⊥平面BCD.
∴∠ADH就是直线AD与平面BCD所成的角.
∵∠ABC=∠DBC=120°,
∴∠ABH=∠DBH=60°.
又AB=DB,
∴△ABH≌△DBH.
∴AH=DH.
∴∠ADH=45°,即AD与平面BCD所成的角为45°.
(2)由△ABH≌△DBH及∠AHB=90°,得∠DHB=90°,即
CB⊥DH.
又CB⊥AH,AH、DH![]() 平面ADH,AH∩DH=H,
平面ADH,AH∩DH=H,
∴CB⊥平面ADH.
又AD![]() 平面ADH,
平面ADH,
∴CB⊥AD.
∴A、D连线与BC所成角为90°.
(3)方法一:作AM⊥BD于点M,连结HM.
∵AH⊥平面BCD,
∴HM是AM在平面BCD上的射影,根据三垂线定理的逆定理,可得BD⊥HM.
∴∠AMH就是二面角A—BD—C的平面角的补角.
设AB=a,根据已知条件在Rt△ABH中,可求得AH=![]() a,BH=
a,BH=![]() ,
,
在Rt△BDH中,DH=AH=![]() a,
a,
∴HM=![]() a.
a.
∴tan∠AMH=![]() =2.
=2.
∴二面角A—BD—C的大小为π-arctan2.
方法二:∵AH⊥平面BCD,
∴△ABD在平面BCD上的射影是△HBD.
设AB=a,则BD=a,BH=![]() ,DH=AH=
,DH=AH=![]() a.∴AD=
a.∴AD=![]() a.
a.
∴等腰△BAD的面积为
![]() ·
·![]() a·
a·![]() ,
,
Rt△BHD的面积为![]() ·
·![]() a·
a·![]() a=
a=![]() a2.
a2.
∴cosθ=![]() .
.
∴二面角A—BD—C的大小为π-arccos![]() .
.

练习册系列答案
相关题目
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)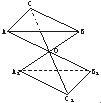 如图,设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O,且
如图,设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O,且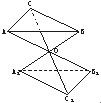
 =
= =
= =
= .试求
.试求 的值.
的值.