题目内容
设一物体从初速度1开始做直线运动,已知在任意时刻t时的加速度为2
解:取物体运动的起点为原点,在t时刻的位移为s=s(t),速度为v=v(t),加速度为a=a(t),则有s′(t)=v(t),v′(t)=a(t)=2![]() +1;
+1;
s(0)=0,v(0)=1.
在时间[0,t]上,有
v(t)-v(0)=![]()
![]()
∴v(t)=![]()
s(t)-s(0)=![]()
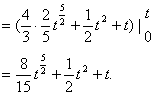
∵s(0)=0,
∴s(t)=![]()
绿色通道:物体做变速直线运动的速度v,等于加速度函数a=a(t)在时间区间[a,b]上的定积分![]() ;物体做变速直线运动经过的路程s,等于其速度函数v=v(t)〔v(t)≥0〕在时间区间[a,b]上的定积分
;物体做变速直线运动经过的路程s,等于其速度函数v=v(t)〔v(t)≥0〕在时间区间[a,b]上的定积分![]()

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目