题目内容
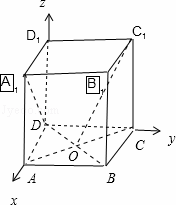
在正方体ABCD﹣A1B1C1D1中,O为AC,BD的交点,则C1O与A1D所成角余弦( )
|
| A. |
| B. | 0 | C. |
| D. |
|
考点:
异面直线及其所成的角.
专题:
计算题;空间角.
分析:
设正方体ABCD﹣A1B1C1D1的棱长为2,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,利用向量法能求出C1O与A1D所成角余弦值.
解答:
解:设正方体ABCD﹣A1B1C1D1的棱长为2,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
则C1(0,2,2),O(1,1,0),A1(2,0,2),D(0,0,0),
∴![]() =(1,﹣1,﹣2),
=(1,﹣1,﹣2),![]() =(﹣2,0,﹣2),
=(﹣2,0,﹣2),
设C1O与A1D所成角为θ,
则cosθ=|cos<![]() ,
,![]() |=|
|=|![]() |=
|=![]() .
.
故选C.
点评:
本题考查异面直线所成角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
在正方体ABCD-A1B1C1D1中,已知E是棱C1D1的中点,则异面直线B1D1与CE所成角的余弦值的大小是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
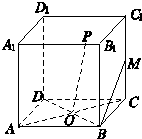 如图,在正方体ABCD-A1B1C1D1中,M是C1C的中点,O是底面ABCD的中心,P是A1B1上的任意点,则直线BM与OP所成的角为
如图,在正方体ABCD-A1B1C1D1中,M是C1C的中点,O是底面ABCD的中心,P是A1B1上的任意点,则直线BM与OP所成的角为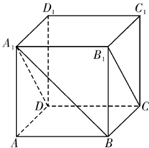 如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于
如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于