题目内容
平面内有一长度为2的线段AB和一动点P满足|PA|+|PB|=6，则|PA|的取值范围是（ ）
分析：依题意，动点P的轨迹是以A，B为焦点，长轴长为6的椭圆，利用椭圆的几何性质即可求得|PA|的取值范围．
解答：解：∵|AB|=2，动点P满足|PA|+|PB|=6，
∴动点P的轨迹是以A，B为焦点，长轴长为6的椭圆，
即2c=2，2a=6，
∴c=1，a=3，
∴|PA|max=a+c=3+1=4，|PA|min=a-c=3-1=2．
∴2≤|PA|≤4．
故选D．
∴动点P的轨迹是以A，B为焦点，长轴长为6的椭圆，
即2c=2，2a=6，
∴c=1，a=3，
∴|PA|max=a+c=3+1=4，|PA|min=a-c=3-1=2．
∴2≤|PA|≤4．
故选D．
点评：本题考查椭圆的定义域简单性质，明确点P的轨迹是以A，B为焦点，长轴长为6的椭圆是关键．属于中档题．
练习册系列答案
相关题目
和一动点
，若满足
，则
的取值范围是（
）
，
则
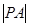的取值范围是：（ ）
