题目内容
某工厂每月生产某种产品三件,经检测发现,工厂生产该产品的合格率为 ,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合格与否相互没有影响.
,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合格与否相互没有影响.
(Ⅰ)求工厂每月盈利额ξ(万元)的所有可能取值;
(Ⅱ)若该工厂制定了每月盈利额不低于40万元的目标,求该工厂达到盈利目标的概率;
(Ⅲ)求工厂每月盈利额ξ的分布列和数学期望.
解:(I)工厂每月生产的三种产品中,合格产品的件数的所有可能结果是:0,1,2,3,则相应的月盈利额ξ的取值量ξ=-30,5,40,75…(2分)
(II)月盈利额ξ的分布量:
P(ξ=-30)=C30( )3=
)3= ,P(ξ=5)=C31(
,P(ξ=5)=C31( )2•
)2• =
= ,
,
P(ξ=40)=C32( )2•
)2• =
=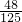 ,P(ξ=75)=C33(
,P(ξ=75)=C33( )3=
)3= ,
,
所以P(ξ≥40)=P(ξ=40)+P(ξ=75)= …(12分)
…(12分)
即
(III)Eξ=(-30)× +5×
+5× +40×
+40×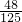 +75×
+75× =54…(14分)
=54…(14分)
分析:(I)由题意知,工厂每月生产的三种产品中,合格产品的件数的所有可能结果是:0,1,2,3,得到相应的月盈利额ξ的取值量ξ=-30,5,40,75.
(II)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列
(III)根据上一问做出的变量的分布列,代入求期望值的公式做出期望值.
点评:本题考查离散型随机变量的分布列和期望,即独立重复试验的概率公式,本题解题的关键是看出所给的变量符合什么规律,利用概率的公式来解题.
(II)月盈利额ξ的分布量:
P(ξ=-30)=C30(
 )3=
)3= ,P(ξ=5)=C31(
,P(ξ=5)=C31( )2•
)2• =
= ,
,P(ξ=40)=C32(
 )2•
)2• =
=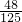 ,P(ξ=75)=C33(
,P(ξ=75)=C33( )3=
)3= ,
,所以P(ξ≥40)=P(ξ=40)+P(ξ=75)=
 …(12分)
…(12分)即
| ξ | -30 | 5 | 40 | 75 |
| P |  |  | 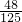 |  |
 +5×
+5× +40×
+40×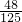 +75×
+75× =54…(14分)
=54…(14分)分析:(I)由题意知,工厂每月生产的三种产品中,合格产品的件数的所有可能结果是:0,1,2,3,得到相应的月盈利额ξ的取值量ξ=-30,5,40,75.
(II)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列
(III)根据上一问做出的变量的分布列,代入求期望值的公式做出期望值.
点评:本题考查离散型随机变量的分布列和期望,即独立重复试验的概率公式,本题解题的关键是看出所给的变量符合什么规律,利用概率的公式来解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目