题目内容
设函数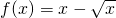 .
.
(1)求使得f(x)>0成立的x的取值范围;
(2)判断f(x)在区间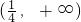 上的单调性,并用定义加以证明.
上的单调性,并用定义加以证明.
(1)解:f(x)>0,即 ,即
,即
∴ ,∴x>1
,∴x>1
∴使得f(x)>0成立的x的取值范围是(1,+∞);
(2)解:f(x)在区间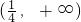 上单调递增,
上单调递增,
证明:设x1>x2> ,则f(x1)-f(x2)=
,则f(x1)-f(x2)= =
=
∵x1>x2> ,∴x1-x2>0,
,∴x1-x2>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴f(x)在区间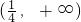 上单调递增.
上单调递增.
分析:(1)将函数代入,解不等式,即可求得使得f(x)>0成立的x的取值范围;
(2)f(x)在区间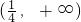 上单调递增,再利用定义加以证明.
上单调递增,再利用定义加以证明.
点评:本题重点考查解不等式,考查函数的单调性的判断与证明,利用定义证明函数单调性的步骤为:取值、作差、变形、定号下结论.
 ,即
,即
∴
 ,∴x>1
,∴x>1∴使得f(x)>0成立的x的取值范围是(1,+∞);
(2)解:f(x)在区间
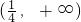 上单调递增,
上单调递增,证明:设x1>x2>
 ,则f(x1)-f(x2)=
,则f(x1)-f(x2)= =
=
∵x1>x2>
 ,∴x1-x2>0,
,∴x1-x2>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴f(x)在区间
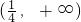 上单调递增.
上单调递增.分析:(1)将函数代入,解不等式,即可求得使得f(x)>0成立的x的取值范围;
(2)f(x)在区间
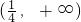 上单调递增,再利用定义加以证明.
上单调递增,再利用定义加以证明.点评:本题重点考查解不等式,考查函数的单调性的判断与证明,利用定义证明函数单调性的步骤为:取值、作差、变形、定号下结论.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 .
. 在
在 上的值域;
上的值域; ,在
,在 上存在唯一的
上存在唯一的 ,使得
,使得 ;
;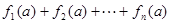 的值.
的值.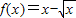 .
. 上的单调性,并用定义加以证明.
上的单调性,并用定义加以证明. .
. 上的单调性,并用定义加以证明.
上的单调性,并用定义加以证明.