题目内容
若函数y=ax与y=-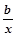 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)
上是( )
| A.增函数 | B.减函数 | C.先增后减 | D.先减后增 |
B
解析

练习册系列答案
相关题目
若函数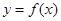 的定义域为
的定义域为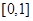 ,则下列函数中可能是偶函数的是
,则下列函数中可能是偶函数的是
A.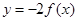 | B.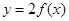 | C. | D.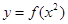 |
已知集合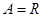 ,
,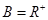 ,f:A→B是从A到B的一个映射,若f:x→2x-1,则B中的元素3的原象为 ( )
,f:A→B是从A到B的一个映射,若f:x→2x-1,则B中的元素3的原象为 ( )
| A.-1 | B.1 | C.2 | D.3 |
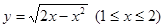 反函数是 ( )
反函数是 ( )
A.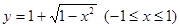 | B.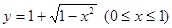 |
C.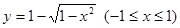 | D.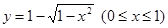 |
已知定义在R上的函数y = f(x)满足下列三个条件:①对任意的x∈R都有
f(x+2)=-f(x);②对于任意的0≤x1<x2≤2 ,都有f(x1)<f(x2),③y=f(x+2)的图象关于y
,都有f(x1)<f(x2),③y=f(x+2)的图象关于y
轴对称,则下列结论中正确的是( )
| A.f(4.5)<f(6.5)<f(7) | B.f(7)<f (6.5)<f(4.5) (6.5)<f(4.5) |
| C.f(7)<f(4.5)<f(6.5) | D.f(4.5)<f(7)<f(6.5) |
函数f(x)=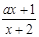 在区间(-2,+∞)上单调递增,则实数a的取值范围是( )
在区间(-2,+∞)上单调递增,则实数a的取值范围是( )
A.(0,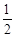 ) ) | B.( 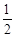 ,+∞) ,+∞) | C.(-2,+∞) | D.(-∞,-1)∪(1,+∞) |
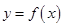 的导函数图象如图所示,则下面判断正确的是
的导函数图象如图所示,则下面判断正确的是 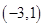 上
上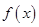 是增函数
是增函数 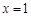 处
处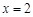 处
处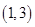 上
上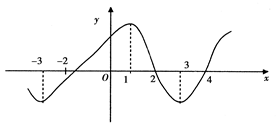
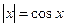 在
在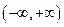 内 ( )
内 ( ) .有且仅有一个根
.有且仅有一个根  C.有且仅有两个根 C.有无穷多个根
C.有且仅有两个根 C.有无穷多个根 ,则
,则 的表达式是( )
的表达式是( ) B
B  C
C  D
D 