题目内容
在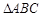 中,已知
中,已知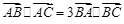 .
.
(1)求证: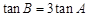 ;
;
(2)若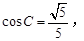 求A的值.
求A的值.
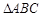 中,已知
中,已知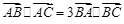 .
.(1)求证:
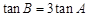 ;
;(2)若
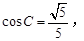 求A的值.
求A的值.(1)见解析(2)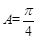 。
。
【考点】平面微量的数量积,三角函数的基本关系式,两角和的正切公式,解三角形。
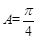 。
。【考点】平面微量的数量积,三角函数的基本关系式,两角和的正切公式,解三角形。
(1)先将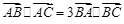 表示成数量积,再根据正弦定理和同角三角函数关系式证明。
表示成数量积,再根据正弦定理和同角三角函数关系式证明。
(2)由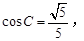 可求
可求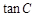 ,由三角形三角关系,得到
,由三角形三角关系,得到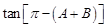 ,从而根据两角和的正切公式和(1)的结论即可求得A的值
,从而根据两角和的正切公式和(1)的结论即可求得A的值
解:(1)∵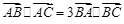 ,∴
,∴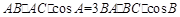 ,即
,即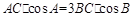 。 由正弦定理,得
。 由正弦定理,得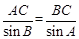 ,∴
,∴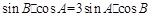 。
。
又∵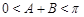 ,∴
,∴ 。∴
。∴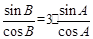 即
即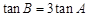 。
。
(2)∵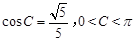 ,∴
,∴ 。∴
。∴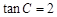 。
。
∴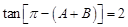 ,即
,即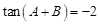 。∴
。∴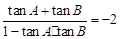 。
。
由 (1) ,得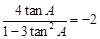 ,解得
,解得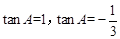 。
。
∵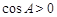 ,∴
,∴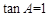 。∴
。∴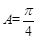
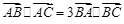 表示成数量积,再根据正弦定理和同角三角函数关系式证明。
表示成数量积,再根据正弦定理和同角三角函数关系式证明。(2)由
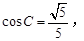 可求
可求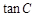 ,由三角形三角关系,得到
,由三角形三角关系,得到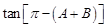 ,从而根据两角和的正切公式和(1)的结论即可求得A的值
,从而根据两角和的正切公式和(1)的结论即可求得A的值解:(1)∵
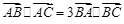 ,∴
,∴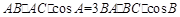 ,即
,即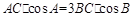 。 由正弦定理,得
。 由正弦定理,得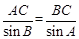 ,∴
,∴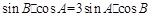 。
。又∵
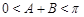 ,∴
,∴ 。∴
。∴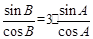 即
即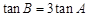 。
。(2)∵
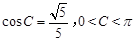 ,∴
,∴ 。∴
。∴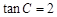 。
。∴
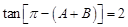 ,即
,即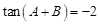 。∴
。∴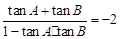 。
。由 (1) ,得
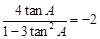 ,解得
,解得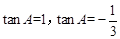 。
。∵
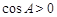 ,∴
,∴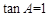 。∴
。∴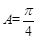

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
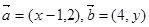 ,若
,若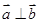 ,则16x+4y的最小值为____ ____。
,则16x+4y的最小值为____ ____。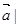 ="8,"
="8," 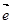 为单位向量,当它们的夹角为
为单位向量,当它们的夹角为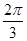 时,
时,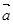 在
在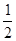
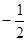
 ,
,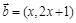 ,
,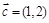 ,且
,且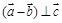 ,则
,则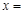 .
.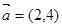 ,
,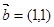 ,若向量
,若向量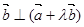 ,则实数
,则实数 的值是 ;
的值是 ;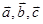 均为单位向量,且
均为单位向量,且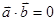 ,
,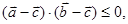 则
则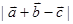 的最大值为( )
的最大值为( )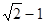
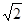
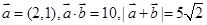 ,则
,则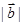 = ;
= ; 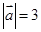 ,
,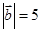 ,若
,若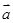 //
//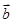 ,则
,则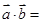 .
.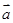 =
= ,
,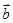 =
=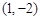 ,
,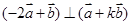 ,则实数
,则实数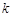 的值是( )
的值是( )