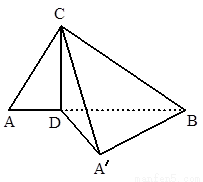题目内容
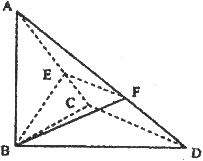
如图,已知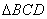 中,
中,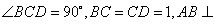 平面
平面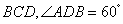 ,
,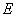 、
、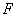 分别是
分别是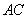 、
、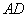 上的动点,且
上的动点,且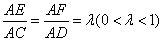
 (1)判断
(1)判断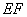 与平面
与平面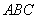 的位置关系并证明:
的位置关系并证明:
(2)若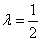 ,求三棱锥
,求三棱锥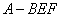 的体积。
的体积。
【答案】
解:(1)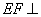 平面
平面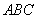
证明:因为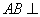 平面
平面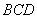 ,所以
,所以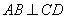 ,
,
又在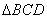 中,
中,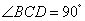 ,所以,
,所以, 又
又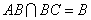
所以,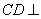 平面
平面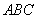 ,
,
又在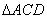 中,
中,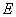 、
、 分别是
分别是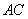 、
、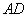 上的动点,且
上的动点,且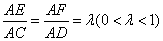
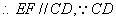
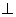 平面
平面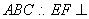 平面
平面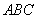 ,
,
所以,不论 为何值,总有
为何值,总有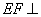 平面
平面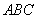 ;
;
(2)解:在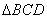 中,
中,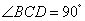 ,
,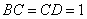 ,所以,
,所以,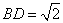
又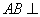 平面
平面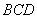 ,所以
,所以 ,
,
又在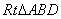 中,
中,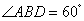 ,
,
由(1)知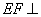 平面
平面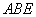 ,
,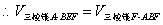
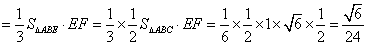
所以,三棱锥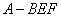 的体积是
的体积是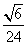

练习册系列答案
相关题目
 、
、 为平面上的两个定点
为平面上的两个定点 ,
, ,且
,且 ,
, (
( 为动点,
为动点, 是
是 和
和 的交点).
的交点).
 、
、 ,且线段
,且线段 的中垂线与直线
的中垂线与直线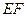 相交于一点
相交于一点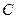 ,证明
,证明 <
< (
( 为
为 中,
中, ,
, 平面
平面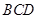 ,
,
 分别为
分别为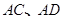 上的动点.
上的动点.  ,求证:平面
,求证:平面 平面
平面 ;
; ,
, ,求平面
,求平面 与平面
与平面
 中,
中, ,
,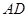 斜边
斜边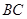 上的高,以
上的高,以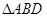 折
起,使
折
起,使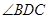 为直角。
为直角。 平面
平面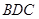 ;(2)求证:
;(2)求证: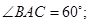
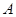 到平面
到平面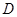 到平面
到平面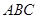 的距离;
的距离;
 中,∠
中,∠ =90°,
=90°,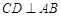 ,且
,且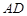 =1,
=1, =2,△
=2,△ 绕
绕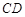 旋转至
旋转至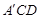 ,使点
,使点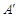 与点
与点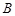 之间的距离
之间的距离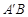 =
=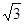 。
。 ⊥平面
⊥平面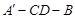 的大小;
的大小;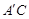 与
与