题目内容
【题目】如图,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() :
:![]()
![]() 的左、右顶点,下顶点和右焦点,直线
的左、右顶点,下顶点和右焦点,直线![]() 过点
过点![]() ,与椭圆
,与椭圆![]() 交于点
交于点![]() ,
,![]() 已知当直线
已知当直线![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若当点![]() 与
与![]() 重合时,点
重合时,点![]() 到椭圆
到椭圆![]() 的右准线的距离为上.
的右准线的距离为上.
①求椭圆![]() 的方程;
的方程;
②求![]() 面积的最大值.
面积的最大值.

【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】分析:(1)先求当直线![]() 轴时,
轴时,![]() ,再根据条件得
,再根据条件得![]() ,最后由
,最后由![]() 解得离心率,(2)设直线
解得离心率,(2)设直线![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() ,联立直线方程与椭圆方程,利用韦达定理化简
,联立直线方程与椭圆方程,利用韦达定理化简![]() ,即得
,即得![]()
![]() ,令
,令![]() ,利用基本不等式求最值,最后考虑特殊情形下三角形面积的值.
,利用基本不等式求最值,最后考虑特殊情形下三角形面积的值.
详解:解:(1)在![]() 中,令
中,令![]()
可得![]() ,所以
,所以![]()
所以当直线![]() 轴时,
轴时,![]()
又![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
(2)① 因为![]() ,所以
,所以![]() ,
,![]()
椭圆方程为![]()
当点![]() 与点
与点![]() 重合时,
重合时,![]() 点坐标为
点坐标为![]()
又![]() ,所以此时直线
,所以此时直线![]() 为
为![]()
由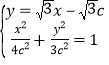 得
得![]()
又![]() ,所以
,所以![]()
所以椭圆方程为![]()
② 设直线![]() 为
为![]()
由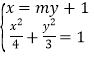 得
得![]()
即![]() ,
,![]() 恒成立
恒成立
设![]() ,
,![]()
则![]()
![]() ,
,![]()
![]()
所以![]()
![]()
![]()
![]()
令![]() ,则
,则![]() 且
且![]()
![]()
![]()
![]()
![]() ,
,![]()
易知函数![]() 在
在![]() 上单调递增
上单调递增
所以当![]() 时,
时,![]()
即![]() 的面积的最大值为
的面积的最大值为![]()

练习册系列答案
相关题目
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为 )
)

