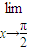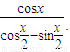题目内容
求下列各极限:(1)
| lim |
| x→2 |
| 4 |
| x2-4 |
| 1 |
| x-2 |
(2)
| lim |
| x→∞ |
| (x+a)(x+b) |
(3)
| lim |
| x→0 |
| x |
| |x| |
(4)
| lim | ||
x→
|
| cosx | ||||
cos
|
分析:(1)把
(
-
)转化成
=
,再进行计算.
(2)把
(
-x)转化为
,再进行计算.
(3)因为
≠
,所以
不存在.
(4)把
.转化为
cos
+sin
)再进行计算.
| lim |
| x→2 |
| 4 |
| x2-4 |
| 1 |
| x-2 |
| lim |
| x→2 |
| 4-(x+2) |
| x2-4 |
| lim |
| x→2 |
| -1 |
| x+2 |
(2)把
| lim |
| x→∞ |
| (x+a)(x+b) |
| lim |
| x→∞ |
| (a+b)x+ab | ||
|
(3)因为
| lim |
| x→0+ |
| x |
| |x| |
| lim |
| x→0- |
| x |
| |x| |
| lim |
| x→0 |
| x |
| |x| |
(4)把
| lim | ||
x→
|
| cosx | ||||
cos
|
| lim | ||
x→
|
| x |
| 2 |
| x |
| 2 |
解答:解:(1)原式=
=
=-
.
(2)原式=
=a+b.
(3)因为
=1,而=
=-1,
≠
,所以
不存在.
(4)原式=
=
(cos
+sin
)=
.
| lim |
| x→2 |
| 4-(x+2) |
| x2-4 |
| lim |
| x→2 |
| -1 |
| x+2 |
| 1 |
| 4 |
(2)原式=
| lim |
| x→∞ |
| (a+b)x+ab | ||
|
(3)因为
| lim |
| x→0+ |
| x |
| |x| |
| lim |
| x→0- |
| x |
| |x| |
| lim |
| x→0+ |
| x |
| |x| |
| lim |
| x→0- |
| x |
| |x| |
| lim |
| x→0 |
| x |
| |x| |
(4)原式=
| lim | ||
x→
|
cos2
| ||||
cos
|
| lim | ||
x→
|
| x |
| 2 |
| x |
| 2 |
| 2 |
点评:若f(x)在x0处连续,则应有
f(x)=f(x0),故求f(x)在连续点x0处的极限时,只需求f(x0)即可;若f(x)在x0处不连续,可通过变形,消去x-x0因式,转化成可直接求f(x0)的式子.
| lim |
| x→x0 |

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
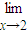 (
(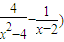 ;
;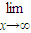 (
(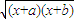 -x);
-x);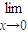
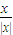 ;
;