题目内容
7.如果${A}_{n}^{5}$=a${C}_{n}^{n-5}$,则a的值是120.分析 根据排列、组合公式,利用阶乘公式,即可求出a的值是多少.
解答 解:∵${A}_{n}^{5}$=a${C}_{n}^{n-5}$,
∴${A}_{n}^{5}$=a${C}_{n}^{5}$;
∴a=$\frac{{A}_{n}^{5}}{{C}_{n}^{5}}$=5!=120.
故答案为:120.
点评 本题考查了排列组合的应用问题,也考查了计算能力的应用问题,是基础题目.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
15.某人练习射击,共有5发子弹,每次击中目标的概率为0.6,若他只需要在五次射击中四次击中目标就算合格,一旦合格即停止练习.则他在第五次射击结束时恰好合格的概率为( )
| A. | 0.64×0.4 | B. | C${\;}_{5}^{4}$•0.64•(1-0.6)+C${\;}_{5}^{5}$•0.65 | ||
| C. | 0.64 | D. | C${\;}_{4}^{3}$×0.64×0.4 |
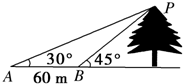 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.