题目内容
已知θ∈R,则
+
的最大值是( )
| 1+sin2θ |
| 1+cos2θ |
分析:把所求式子平方,利用完全平方公式化简后,再根据同角三角函数间的基本关系及二倍角的正弦、余弦函数公式化简,把被开方数化为一个角的余弦函数,根据余弦函数的值域,即可得到所求式子平方的最大值,开方即可求出所求式子的最大值.
解答:解:(
+
)2
=1+sin2θ+1+cos2θ+2
=3+2
=3+2
=3+2
,
∵-1≤cos4θ≤1,
∴当cos4θ=-1时,(
+
)2取得最大值,
最大值为3+2
=6,
则
+
的最大值是
.
故选D
| 1+sin2θ |
| 1+cos2θ |
=1+sin2θ+1+cos2θ+2
| (1+sin2θ)(1+cos2θ) |
=3+2
2+
|
=3+2
2+
|
=3+2
|
∵-1≤cos4θ≤1,
∴当cos4θ=-1时,(
| 1+sin2θ |
| 1+cos2θ |
最大值为3+2
|
则
| 1+sin2θ |
| 1+cos2θ |
| 6 |
故选D
点评:此题考查了三角函数的化简求值,涉及的知识有:同角三角函数间的基本关系,二倍角的正弦、余弦函数公式,以及余弦函数的值域,把所求式子平方,利用三角函数的恒等变形把被开方数化为一个角的余弦函数是解本题的关键.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
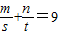 ,其中m、n是常数,当s+t取最小
,其中m、n是常数,当s+t取最小 时,m、n对应的点(m,n)是双曲线
时,m、n对应的点(m,n)是双曲线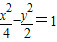 一条弦的中点,则此弦所在的直线方程为( )
一条弦的中点,则此弦所在的直线方程为( )