题目内容
已知曲线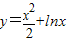
的一条切线的斜率为2，则此切线方程为（ ）A．2x+y+1=0
B．4x+2y-3=0
C．4x-2y-3=0
D．2x-y-1=0
【答案】分析：直接利用函数导数值为2，求出x值，求出切点的坐标，然后求出切线方程．
解答：解：因为曲线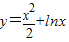
的导数为：
，
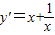所以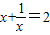
，解得x=1，所以y=
，
切线方程为：y-
=2（x-1），
即4x-2y-3=0．
故选C．
点评：本题是基础题，考查函数的导数的应用，切线方程的求法，考查计算能力．
解答：解：因为曲线
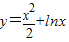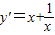的导数为：，所以
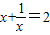，解得x=1，所以y=，切线方程为：y-
=2（x-1），即4x-2y-3=0．
故选C．
点评：本题是基础题，考查函数的导数的应用，切线方程的求法，考查计算能力．
练习册系列答案
轻松暑假总复习系列答案
相关题目
的一条切线的斜率为
，则切点的横坐标为 （ ）
的一条切线的斜率为
，则切点的横坐标为（ ）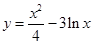
的一条切线的斜率为
，则该切线的切点横坐标为
B.
C.
D.
的一条切线的斜率为2，则该切线的方程为
。
的一条切线的斜率为
,则切点的纵坐标为 ▲