题目内容
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A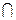 B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A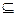 CRB,求实数m的取值范围
CRB,求实数m的取值范围
(Ⅰ)若A
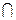 B=[0,3],求实数m的值
B=[0,3],求实数m的值(Ⅱ)若A
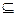 CRB,求实数m的取值范围
CRB,求实数m的取值范围 解:由已知得:A={x|-1≤x≤3},B={x|m-2≤x≤m+2}
解:由已知得:A={x|-1≤x≤3},B={x|m-2≤x≤m+2}(Ⅰ)∵A
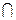 B=[
B=[ 0,3],∴
0,3],∴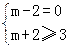 ,∴
,∴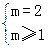 ,∴m=2. …………7分
,∴m=2. …………7分(Ⅱ)CRB={x|x<m-2或x>m+2},∵A
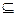 CRB,∴m-2>3,或m+2<-1,
CRB,∴m-2>3,或m+2<-1,∴m的取值范围为(-∞,-3)
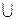 (5,+∞).…………………………14分
(5,+∞).…………………………14分略

练习册系列答案
相关题目
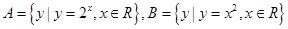 ,则 ( )
,则 ( )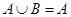
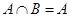
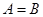
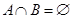
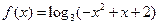 的定义域为集合
的定义域为集合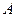 ,
,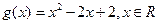 的值域为集合
的值域为集合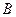 ,
,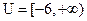 . (1)求
. (1)求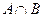 、
、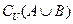 .
.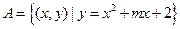 ,
,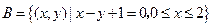 .
.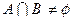 ,求实数
,求实数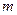 的取值范围.
的取值范围.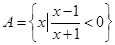 ,
,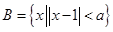 ,则“
,则“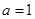 ”是“
”是“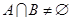 ”的( )
”的( )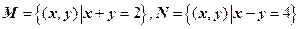 ,那么集合
,那么集合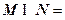 ▲__
▲__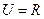 ,集合
,集合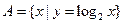 ,
,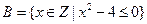 ,则下列结论正确的是( )
,则下列结论正确的是( )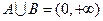
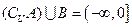
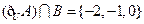
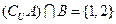
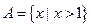 ,
,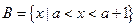 .
.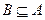 ,求实数
,求实数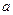 的取值范围;
的取值范围;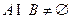 ,求实数
,求实数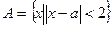 ,
,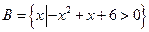 ,若
,若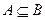 ,
,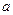 的取值范围是_______ ______
的取值范围是_______ ______