题目内容
 (2013•浙江)如图,点P(0,-1)是椭圆C1:
(2013•浙江)如图,点P(0,-1)是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
分析:(1)由题意可得b=1,2a=4,即可得到椭圆的方程;
(2)设A(x1,y1),B(x2,y2),D(x0,y0).由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx-1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|,又l2⊥l1,可得直线l2的方程为x+kx+k=0,与椭圆的方程联立即可得到点D的横坐标,即可得出|PD|,即可得到三角形ABD的面积,利用基本不等式的性质即可得出其最大值,即得到k的值.
(2)设A(x1,y1),B(x2,y2),D(x0,y0).由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx-1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|,又l2⊥l1,可得直线l2的方程为x+kx+k=0,与椭圆的方程联立即可得到点D的横坐标,即可得出|PD|,即可得到三角形ABD的面积,利用基本不等式的性质即可得出其最大值,即得到k的值.
解答:解:(1)由题意可得b=1,2a=4,即a=2.
∴椭圆C1的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),D(x0,y0).
由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx-1.
又圆C2:x2+y2=4的圆心O(0,0)到直线l1的距离d=
.
∴|AB|=2
=2
.
又l2⊥l1,故直线l2的方程为x+ky+k=0,联立
,消去y得到(4+k2)x2+8kx=0,解得x0=-
,
∴|PD|=
.
∴三角形ABD的面积S△=
|AB|•|PD|=
.
∴S=
≤
=
,当且仅当k=±
时取等号,
故所求直线l1的方程为y=±
x-1.
∴椭圆C1的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),D(x0,y0).
由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx-1.
又圆C2:x2+y2=4的圆心O(0,0)到直线l1的距离d=
| 1 | ||
|
∴|AB|=2
| 4-d2 |
|
又l2⊥l1,故直线l2的方程为x+ky+k=0,联立
|
| 8k |
| 4+k2 |
∴|PD|=
8
| ||
| 4+k2 |
∴三角形ABD的面积S△=
| 1 |
| 2 |
8
| ||
| 4+k2 |
∴S=
| 32 | ||||||
|
| 32 | ||||||||
2
|
16
| ||
| 13 |
| ||
| 2 |
故所求直线l1的方程为y=±
| ||
| 2 |
点评:本题主要考查了椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识,同时考查了推理能力和计算能力及分析问题和解决问题的能力.

练习册系列答案
相关题目
 (2013•浙江模拟)如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1 (x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
(2013•浙江模拟)如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1 (x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( ) (2013•浙江)如图F1、F2是椭圆C1:
(2013•浙江)如图F1、F2是椭圆C1: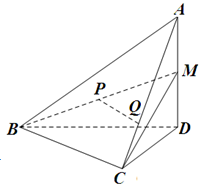 (2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,
(2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD, (2013•浙江)如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=
(2013•浙江)如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=