题目内容
如果在一次试验中,某事件A发生的概率为p,那么在n次独立重复试验中,事件A发生偶数次的概率为 .
【答案】分析:事件A发生偶数次的概率为 Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…,而把[(1-p)+p]n和[(1-p)-p]n的展开式相加并除以2,即可得到事件A发生偶数次的
概率.
解答:解:事件A发生偶数次的概率为 Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…
又[(1-p)+p]n=Cnp(1-p)n+Cn1p1(1-p)n-1+Cn2p2(1-p)n-2+Cn3p3(1-p)n-3+Cn4p4(1-p)n-4+…+Cnnpn(1-p) ①,
[(1-p)-p]n=Cnp(1-p)n-Cn1p1(1-p)n-1+Cn2p2(1-p)n-2-Cn3p3(1-p)n-3+Cn4p4(1-p)n-4+…+(-1)nCnnpn(1-p) ②,
由①+②并除以2 可得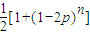 =Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…,
=Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…,
故答案为: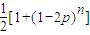 .
.
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,二项式定理的应用,得到[(1-p)+p]n和[(1-p)-p]n的展开式,是解题的关键,属于中档题.
概率.
解答:解:事件A发生偶数次的概率为 Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…
又[(1-p)+p]n=Cnp(1-p)n+Cn1p1(1-p)n-1+Cn2p2(1-p)n-2+Cn3p3(1-p)n-3+Cn4p4(1-p)n-4+…+Cnnpn(1-p) ①,
[(1-p)-p]n=Cnp(1-p)n-Cn1p1(1-p)n-1+Cn2p2(1-p)n-2-Cn3p3(1-p)n-3+Cn4p4(1-p)n-4+…+(-1)nCnnpn(1-p) ②,
由①+②并除以2 可得
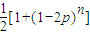 =Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…,
=Cnp(1-p)n+Cn2p2(1-p)n-2+Cn4p4(1-p)n-4+…,故答案为:
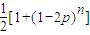 .
.点评:本题主要考查n次独立重复实验中恰好发生k次的概率,二项式定理的应用,得到[(1-p)+p]n和[(1-p)-p]n的展开式,是解题的关键,属于中档题.

练习册系列答案
相关题目