题目内容
已知数列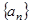 中,对一切自然数
中,对一切自然数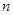 ,都有
,都有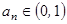 且首项为
且首项为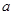 ,
,
若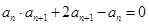 。
。
(1)用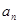 表示
表示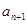 ,并求数列
,并求数列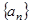 的通项公式;
的通项公式;
(2)若 表示数列
表示数列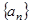 的前
的前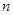 项之和,则
项之和,则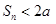 。
。
【答案】
(1)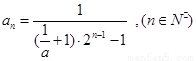 ;(2)
;(2) 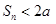 。
。
【解析】本试题主要是考查了递推关系式的运用以及数列求和的综合运用。
(1)因为由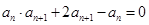 ,得
,得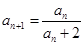 ,故
,故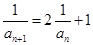 ,从而得到关系式;
,从而得到关系式;
(2)由条件可得: ,则
,则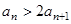 ,即
,即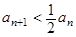 ,利用放缩法得到证明。
,利用放缩法得到证明。
解:(1)由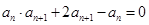 ,得
,得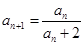 ,故
,故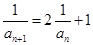 ,
,
记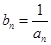 ,则
,则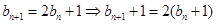 ,再记
,再记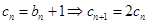 ,
,
且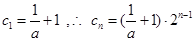 ,
,
所以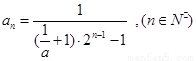
(2)由条件可得: ,则
,则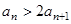 ,即
,即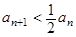
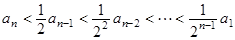 ,即
,即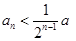 ,于是有,
,于是有,
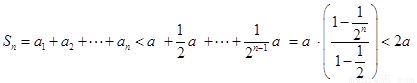 ,即
,即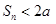 。
。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
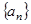 中,对一切自然数
中,对一切自然数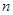 ,都有
,都有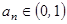 且
且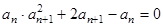 .
.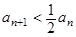 ;
;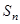 表示数列
表示数列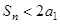 .
.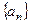 中,对一切自然数
中,对一切自然数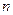 ,都有
,都有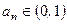 且
且 .
.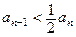 ;
; 表示数列
表示数列 .
.