题目内容
函数 ,则该函数为( )
,则该函数为( )A.单调递增函数,奇函数
B.单调递增函数,偶函数
C.单调递减函数,奇函数
D.单调递减函数,偶函数
【答案】分析:可得f(0)=0,当x≥0时,f(x)单调递增;当x≤0时,f(x)单调递增.所以f(x)单调递增.又可得f(-x)=-f(x),故为奇函数.
解答:解:由题意可得f(0)=0,且x≥0时,f(x)单调递增;
当x≤0时,f(x)单调递增.所以f(x)单调递增.
又∵ ,
,
∴f(-x)=-f(x),所以f(x)为奇函数.
故选A.
点评:本题考查函数单调性的判断与证明,属基础题.
解答:解:由题意可得f(0)=0,且x≥0时,f(x)单调递增;
当x≤0时,f(x)单调递增.所以f(x)单调递增.
又∵
 ,
,∴f(-x)=-f(x),所以f(x)为奇函数.
故选A.
点评:本题考查函数单调性的判断与证明,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则该函数为( )
,则该函数为( ) ,则该函数为( )
,则该函数为( )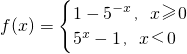 ,则该函数为
,则该函数为 ,则该函数为( )
,则该函数为( )