题目内容
(本小题满分10分)已知直线l的方程为3x+4y-12="0," 求直线m的方程, 使得:
(1)m与l平行, 且过点(-1,3) ;
(2) m与l垂直, 且m与两轴围成的三角形面积为4.
解: (1) 由条件, 可设l′的方程为 3x+4y+m="0," 以x=-1, y=3代入,
得 -3+12+m="0," 即得m=-9, ∴直线l′的方程为 3x+4y-9="0; " 5分
(2) 由条件, 可设l′的方程为4x-3y+n="0," 令y="0," 得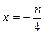 , 令x="0," 得
, 令x="0," 得 , 于是由三角形面积
, 于是由三角形面积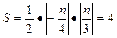 , 得n2="96," ∴
, 得n2="96," ∴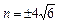 8分
8分
∴直线l′的方程是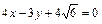 或
或 10分
10分
得 -3+12+m="0," 即得m=-9, ∴直线l′的方程为 3x+4y-9="0; " 5分
(2) 由条件, 可设l′的方程为4x-3y+n="0," 令y="0," 得
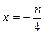 , 令x="0," 得
, 令x="0," 得 , 于是由三角形面积
, 于是由三角形面积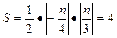 , 得n2="96," ∴
, 得n2="96," ∴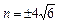 8分
8分∴直线l′的方程是
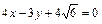 或
或 10分
10分略

练习册系列答案
相关题目
 与直线
与直线 垂直,则
垂直,则 等于( )
等于( )

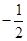
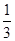
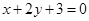 在
在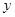 轴上的截距为 ( )
轴上的截距为 ( )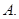
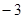
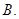
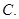
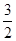
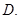
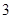
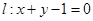 的倾斜角的大小为( )
的倾斜角的大小为( )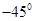
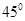
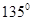
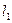 :
: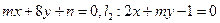 ,分别由下列条件确定
,分别由下列条件确定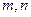 值 (12分)
值 (12分)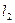 相交于点
相交于点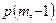
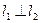 ,且
,且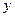 上轴截距为-1
上轴截距为-1 的倾斜角为( )
的倾斜角为( )



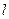 的斜率为
的斜率为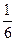 ,且和坐标轴围成面积为3的三角形,求直线
,且和坐标轴围成面积为3的三角形,求直线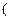 -1,2
-1,2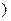 ,B
,B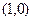 且倾斜角是直线
且倾斜角是直线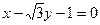 的倾斜角的两倍的直线方程是 ▲ .(直线方程写为一般式)
的倾斜角的两倍的直线方程是 ▲ .(直线方程写为一般式)