题目内容
某地区1986年以来人口总数和居民住宅总面积分别按等比数列和等差数列逐年递增.已知1986年底人均住房面积为10m2,2006年底人均住房面积为20m2.据此计算:
(1)1996年底人均住房面积超过14m2,试给出证明;
(2)若人口年平均增长率不超过3%,能否确保2008年底人均住房面积比2006年底有所增加?为什么?
解:(1)设86年底人口总数为a,住宅总面积10a,年人口增长的公比为q(即后一年是前一年人口的q倍),年住宅总面积的公差为d,则2006年底人均住房面积为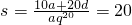 ,则10d=5(2q20-1)a,
,则10d=5(2q20-1)a,
故1996年底人均住房面积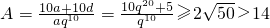 .
.
(2)2008年底人均住房面积 ,
,
2008年与2006年底人均住房面积之差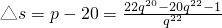 .
.
∵q>0,∴只需考虑分子f(q)=22q20-20q22-1=2q20(11-10q2)-1(q>1).
∵f'(q)=440(q19-q21)<0,∴f(q)单调递减.
又q≤1.03,∴f(q)≥f(1.03)=2×1.0320(11-10×1.032)-1,
∴11-10×1.032>0.39,2×1.0320=2×(1+0.03)20>2×(1+20×0.03)=3.2.
∴f(q)>3.2×0.39-1>0.
此即表明,2008年底人均住房面积仍超过2006年底人均住房面积.
分析:(1)根据人口总数和居民住宅总面积分别按等比数列和等差数列逐年递增,可得2006年底人均住房面积,进而可得1996年底人均住房面积,故可证.
(2)线计算2008年与2006年底人均住房面积之差再利用导数的方法,即可解决.
点评:本题以数列为载体,考查实际运用,关键是正确理解数列模型,从而构建代数式,有一定的综合性.
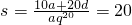 ,则10d=5(2q20-1)a,
,则10d=5(2q20-1)a,故1996年底人均住房面积
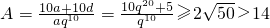 .
.(2)2008年底人均住房面积
 ,
,2008年与2006年底人均住房面积之差
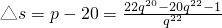 .
.∵q>0,∴只需考虑分子f(q)=22q20-20q22-1=2q20(11-10q2)-1(q>1).
∵f'(q)=440(q19-q21)<0,∴f(q)单调递减.
又q≤1.03,∴f(q)≥f(1.03)=2×1.0320(11-10×1.032)-1,
∴11-10×1.032>0.39,2×1.0320=2×(1+0.03)20>2×(1+20×0.03)=3.2.
∴f(q)>3.2×0.39-1>0.
此即表明,2008年底人均住房面积仍超过2006年底人均住房面积.
分析:(1)根据人口总数和居民住宅总面积分别按等比数列和等差数列逐年递增,可得2006年底人均住房面积,进而可得1996年底人均住房面积,故可证.
(2)线计算2008年与2006年底人均住房面积之差再利用导数的方法,即可解决.
点评:本题以数列为载体,考查实际运用,关键是正确理解数列模型,从而构建代数式,有一定的综合性.

练习册系列答案
相关题目