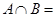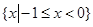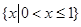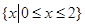题目内容
设集合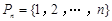 ,
,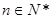 .记
.记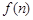 为同时满足下列条件的集合
为同时满足下列条件的集合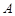 的个数:
的个数:
①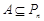 ;②若
;②若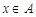 ,则
,则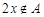 ;③若
;③若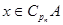 ,则
,则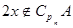 。
。
(1)求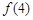 ;
;
(2)求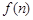 的解析式(用
的解析式(用 表示).
表示).
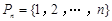 ,
,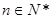 .记
.记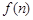 为同时满足下列条件的集合
为同时满足下列条件的集合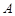 的个数:
的个数:①
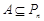 ;②若
;②若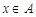 ,则
,则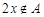 ;③若
;③若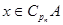 ,则
,则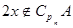 。
。(1)求
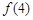 ;
;(2)求
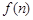 的解析式(用
的解析式(用 表示).
表示).(1)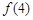 =4。
=4。
( 2 )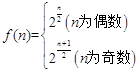 。
。
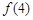 =4。
=4。( 2 )
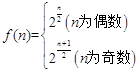 。
。(1)找出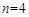 时,符合条件的集合个数即可。
时,符合条件的集合个数即可。
(2)由题设,根据计数原理进行求解
解:(1)当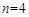 时,符合条件的集合
时,符合条件的集合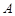 为:
为: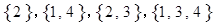 ,
,
∴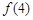 =4。
=4。
( 2)任取偶数 ,将
,将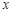 除以2 ,若商仍为偶数.再除以2 ,··· 经过
除以2 ,若商仍为偶数.再除以2 ,··· 经过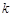 次以后.商必为奇数.此时记商为
次以后.商必为奇数.此时记商为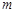 。于是
。于是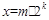 ,其中
,其中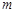 为奇数
为奇数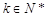 。
。
由条件知.若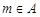 则
则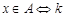 为偶数;若
为偶数;若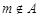 ,则
,则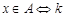 为奇数。
为奇数。
于是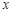 是否属于
是否属于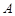 ,由
,由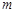 是否属于
是否属于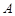 确定。
确定。
设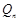 是
是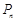 中所有奇数的集合.因此
中所有奇数的集合.因此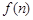 等于
等于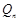 的子集个数。
的子集个数。
当 为偶数〔 或奇数)时,
为偶数〔 或奇数)时,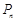 中奇数的个数是
中奇数的个数是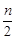 (
( )。
)。
∴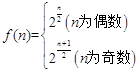
【考点】集合的概念和运算,计数原理。
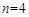 时,符合条件的集合个数即可。
时,符合条件的集合个数即可。(2)由题设,根据计数原理进行求解
解:(1)当
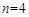 时,符合条件的集合
时,符合条件的集合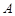 为:
为: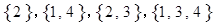 ,
,∴
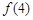 =4。
=4。( 2)任取偶数
 ,将
,将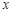 除以2 ,若商仍为偶数.再除以2 ,··· 经过
除以2 ,若商仍为偶数.再除以2 ,··· 经过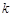 次以后.商必为奇数.此时记商为
次以后.商必为奇数.此时记商为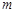 。于是
。于是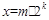 ,其中
,其中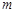 为奇数
为奇数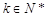 。
。由条件知.若
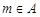 则
则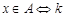 为偶数;若
为偶数;若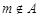 ,则
,则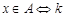 为奇数。
为奇数。于是
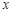 是否属于
是否属于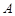 ,由
,由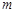 是否属于
是否属于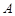 确定。
确定。设
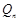 是
是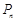 中所有奇数的集合.因此
中所有奇数的集合.因此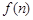 等于
等于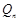 的子集个数。
的子集个数。当
 为偶数〔 或奇数)时,
为偶数〔 或奇数)时,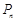 中奇数的个数是
中奇数的个数是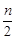 (
( )。
)。∴
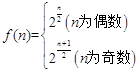
【考点】集合的概念和运算,计数原理。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
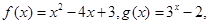 集合
集合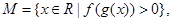
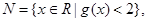 则
则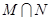 为
为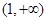
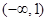
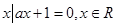 },B={
},B={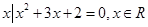 ,}若
,}若 则
则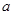 取值集合
取值集合 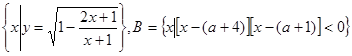 ,分别根据下列条件,求实数
,分别根据下列条件,求实数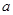 的取值范围(1)
的取值范围(1)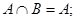 (2)
(2)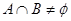
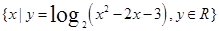 , B=
, B=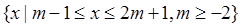 .
.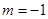 ,求A∩B,
,求A∩B,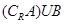 ;
;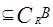 ,求实数m的取值范围。
,求实数m的取值范围。 ,
, ,那么
,那么 .
. 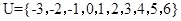 , 集合
, 集合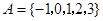 ,
,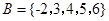 ,则
,则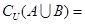 ( )
( )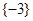
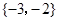
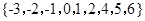
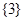
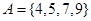 ,
,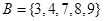 ,全集U=A∪B,则集合
,全集U=A∪B,则集合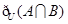 =( )
=( )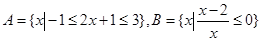 ,则
,则